2. 二叉树

1. 二叉树基本概念

1. 节点

  1. 节点
  2. 根节点
  3. 父节点
  4. 子节点
  5. 兄弟节点

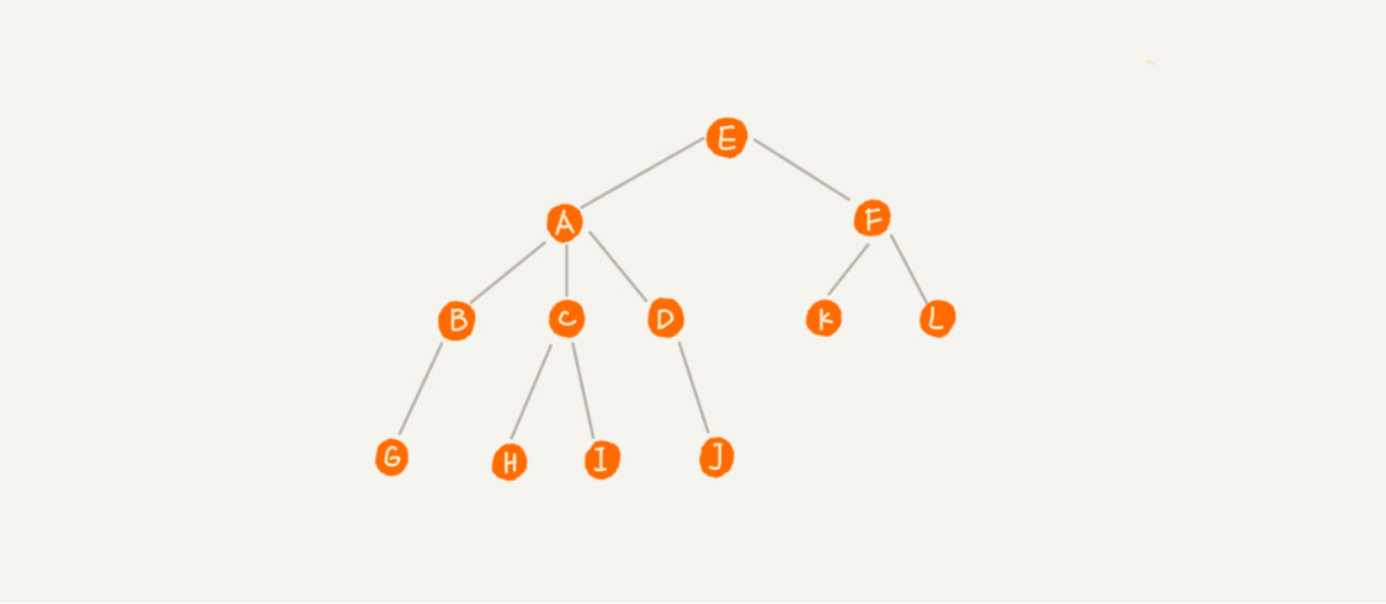
树结构示意图

上图中，A 节点就是 B 节点的父节点，B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点，所以它们之间互称为兄弟节点。我们把没有父节点的节点叫作根节点，也就是图中的节点 E。我们把没有子节点的节点叫作叶子节点或者叶节点，比如图中的 G、H、I、J、K、L 都是叶子节点。

一棵树没有任何节点，称为空树

一棵树可以只有一个节点，也就是根节点

子树， 左子树， 右子树

2. 度

  • 节点的度(degree): 子树的个数

  • 树的度： 所有节点度中的最大值

  • 叶子节点(leaf): 度为0的节点

  • 非叶子节点：度不为0的节点

3. 层数 和 深度

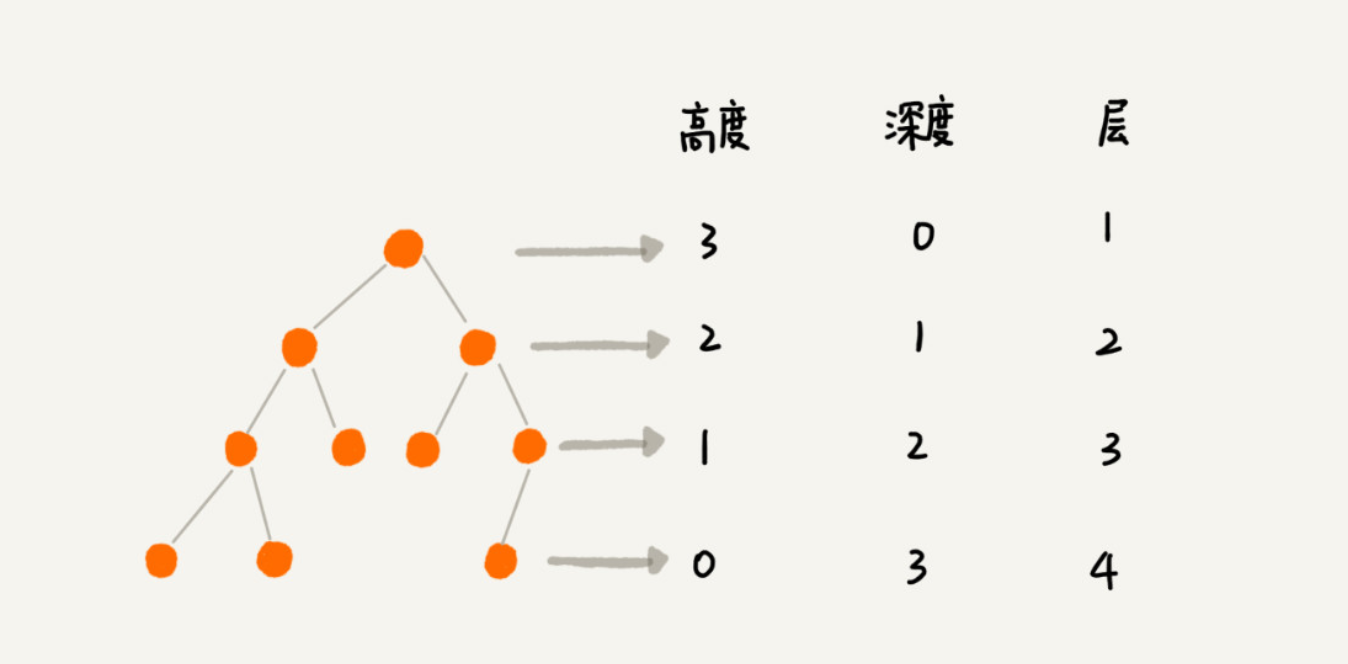
高度、深度、层

  • 层数：根节点在第一层， 根节点的子节点在第二层，以此类推(也有从0层计算)

  • 节点的深度：从根节点到当前节点的唯一路径上的节点总数

  • 节点的高度：从当前节点到最远叶子节点的路径上的节点总数(边数)

  • 树的深度：所有节点深度中的最大值

  • 树的高度：所有节点高度的最大值

  • 树的深度等于树的高度

4. 有序树、无序树、森林

  • 有序树
    • 树种任意节点的子节点之间有顺序关系
  • 无序树
    • 树中任意节点的子节点之间没有顺序关系
    • 也称为“自由树”
  • 森林
    • 由$m \ge 0$棵互不相交的树组成的集合

5. 二叉树 Binary Tree

  • 二叉树的特点

    • 每个节点的度最大为2(最多有2棵子树)

    • 左子树和右子树是由顺序的

    • 即使某节点只有一棵子树，也要分左右子树

    • 二叉树是有序树

  • 二叉树的性质

    • 非空二叉树的第$i$层，最多有$2^{i-1} \quad (i \ge 1)$个节点

    • 在高度为$h$的二叉树上最多有$2^h - 1$个节点(1, 2, 4…的等比数列求和)

    • 对于一棵非空二叉树，如果叶子节点个数为$n_0$，度为2的节点个数为$n_2$，那么$n_0 = n_2 + 1$

      • 证明：

        ​ 假设度为1的节点个数为$n_1$，那么二叉树的节点总数为$n = n_0 + n_1 + n_2$；

        ​ 二叉树的边数为：$n_1 + 2 * n_2= \text{除了根节点，每个节点都有一条边} = n - 1= n_0+n_1+n_2$即$n_0 = n_2+1$.

6. 真二叉树 Proper Binary Tree

graph TB;
1((1))==>2((2))
1((1))==>3((3))
2((2))==>4((4))
2((2))==>5((5))
5((5))==>6((6))
5((5))==>7((7))

所有节点的度要么为0要么为2，才为真二叉树。

7. 满二叉树 Full Binary Tree

所有节点的度要么为0，要么为2，且所有叶子节点都在最后一层

graph TB;
1((1))==>2((2))
1((1))==>3((2))
2((2))==>4((4))
2((2))==>5((5))
3((3))==>6((6))
3((3))==>7((7))
  • 在同样高度的二叉树中，满二叉树的叶子节点数量最多、总结点数量最多
  • 满二叉树一定是真二叉树，真二叉树不一定是满二叉树
  • 假设满二叉树的高度为$h(h \ge 1)$，那么：
    • 第$i$层的节点数量为：$2^{i-1}$
    • 叶子节点数量: $2^{h-1}$
    • 总结点数量：$2^0+2^1 + \cdots + 2^{h-1}=2^{h}-1$

8. 完全二叉树 Complete Binary Tree

叶子节点只会出现最后2层，且最后一层的叶子节点都靠左对齐

graph TB;
1((A))==>2((B))
1((A))==>3((C))
2((B))==>4((D))
2((B))==>5((E))
3((C))==>6((F))
3((C))==>7((G))
4((D))==>8((H))
4((D))==>9((I))
5((E))==>10((J))

性质：

  1. 度为1的节点只有左子树
  2. 度为1的节点要么是1个要么是0个
  3. 同样节点数量的二叉树，完全二叉树的高度最小

  4. 假设完全二叉树的高度为$h(h \ge 1)$，那么：

    • 至少有$2^{h-1}$个节点 $2^0+2^1+\cdots+2^{h-1}+1$
    • 最多有$2^h-1$个节点 $2^0+2^1+ \cdots + 2^{h-1}$满二叉树
    • 总结点数量为$n$。其中$2^{h-1} \le n \le 2^{h}$，即$h-1 \le log_2n \le h$，因为$h$是整数，所以$h=log_2 n向下取整+1=floor(log_2 n) + 1$

  5. 一棵有$n$个节点的完全二叉树 $n > 0$ ，从上到下，从左到右对节点从1开始进行编号，对任意第$i$个节点：

      graph TB;
1((1))==>2((2))
1((1))==>3((3))
2((2))==>4((4))
2((2))==>5((5))
3((3))==>6((6))
3((3))==>7((7))
4((4))==>8((8))
4((4))==>9((9))
5((5))==>10((10))

    • 如果$i=1$，它是根节点
    • 如果$i>1$,它的父节点编号为$floor(1/2)$
    • 如果$2i \le n$,它的左子节点编号为$2i$
    • 如果$2i > n$，它无左子节点
    • 如果$2i+1 \le n$,它的右子节点编号为$2i+1$
    • 如果$2i+1 > n$,它无右子节点

  6. 一棵有$n$个节点的完全二叉树 $n > 0$ ，从上到下，从左到右对节点从0开始进行编号，对任意第$i$个节点：

      graph TB;
1((0))==>2((1))
1((0))==>3((2))
2((1))==>4((3))
2((1))==>5((4))
3((2))==>6((5))
3((2))==>7((6))
4((3))==>8((7))
4((3))==>9((8))
5((4))==>10((9))

    • 如果$i=0$，它是根节点
    • 如果$i>0$,它的父节点编号为$floor((i-1)/2)$
    • 如果$2i + 1\le n-1$,它的左子节点编号为$2i+1$
    • 如果$2i +1> n-1$，它无左子节点
    • 如果,它的右子节点编号为
    • 如果,它无右子节点

满二叉树和完全二叉树

上图中，编号 2 的二叉树中，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树。

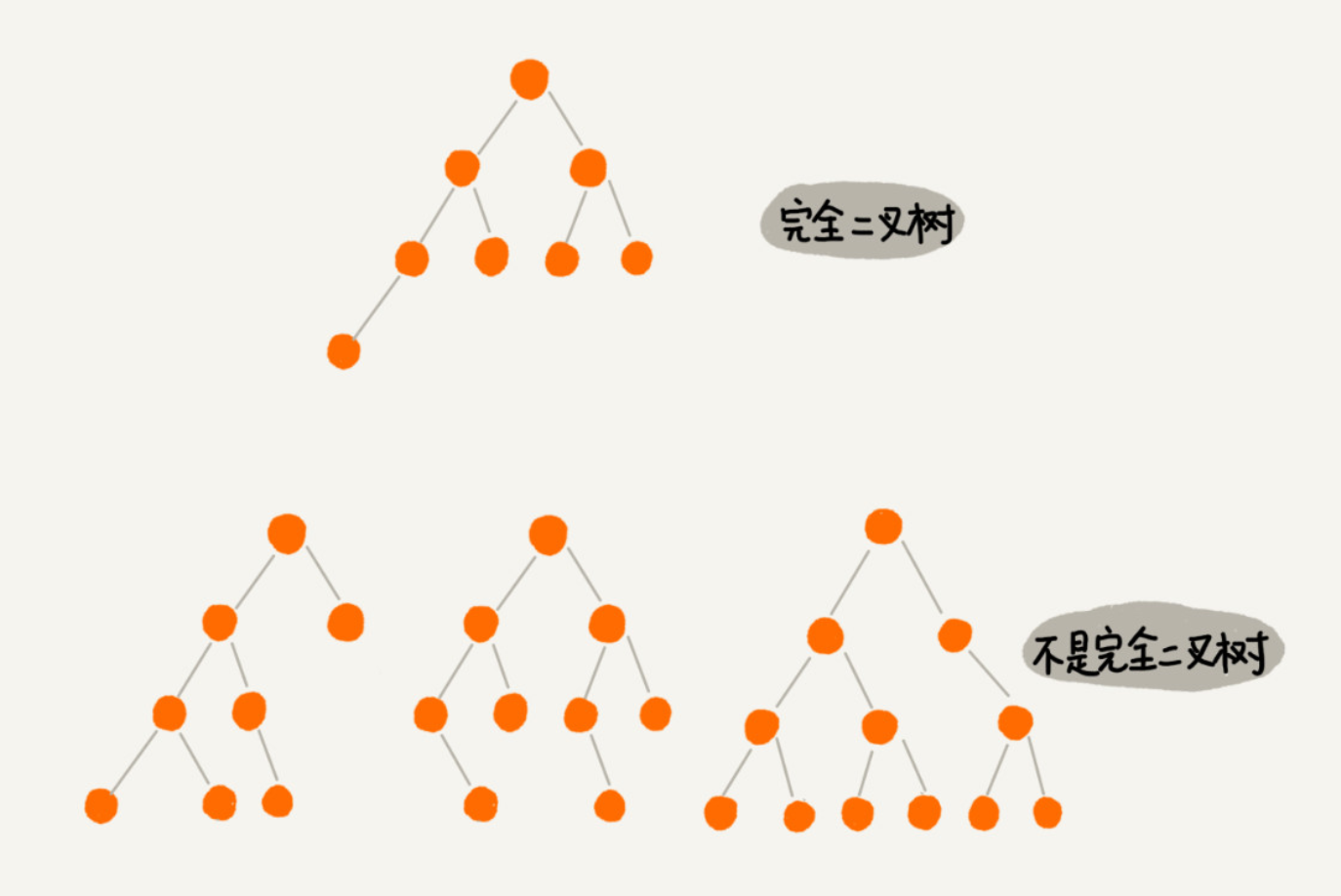
编号 3 的二叉树中，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树。

满二叉树很好理解，也很好识别，但是完全二叉树，有的人可能就分不清了。我画了几个完全二叉树和非完全二叉树的例子，你可以对比着看看。

完全二叉树?

题目：一棵完全二叉树有768个节点，求叶子节点数?

  • 假设叶子节点的个数为, 度为1的节点个数为， 度为2的节点个数为
    • ​ 那么总结点个数为,而。所以。
  • 完全二叉树的，要么为0，要么为1；
    • 当为1时， , 必然是偶数。此时叶子节点个数为， 非叶子节点个数为。
    • 当为0时， , 必然是奇数。此时叶子节点个数为， 非叶子节点个数为。

总结：

  • 叶子节点个数
  • 非叶子节点个数 floor向下取整， ceiling向上取整

因此上题中叶子节点的个数为384

2. 二叉搜索树

1. 二叉搜索树 Binary Search Tree

二叉搜索树是二叉树的一种，是应用非常广泛的一种二叉树，简称BST

  1. 又称作：二叉查找树、二叉排序树树
  2. 任意一个节点的值都大于其左子树所有节点
  3. 任意一个节点的值都小于其右子树所有节点
  4. 它的左右子树也是一棵二叉搜索树

二叉搜索树

可视化网址

二叉搜索树可以提高搜索效率，但其存储元素必须是可比较对象。不允许其元素为None

2. 二叉树设计

  1. 添加 遇到值相等，覆盖或者直接return
    • 找到父节点parent
    • 创建新节点node
    • parent.left = node 或 parent.right= node

3. 二叉树的遍历

1. 前序遍历 (Preorder Traversal)

graph TB;
1((7))==>2((4))
1((7))==>3((9))
2((4))==>4((2))
2((4))==>5((5))
3((9))==>6((8))
3((9))==>7((11))
4((2))==>8((1))
4((2))==>9((3))
7((11))==>10((10))
7((11))==>11((12))

访问顺序：

  1. 根节点
  2. 前序遍历左子树
  3. 前序遍历右子树

上面树的访问顺序为：

2. 中序遍历(Inorder Traversal)

访问顺序：(根节点必须放中间，可以先右后左)

  1. 中序遍历左子树
  2. 中序遍历根节点
  3. 中序遍历右子树

上面树的访问顺序为：。对于二叉搜索树，从小到大顺序排列，升序。如果先右后左，就变为降序。

3. 后序遍历(Postorder Traversal)

访问顺序：(根节点放最后，左右子树可以互换)

  1. 后序遍历左子树
  2. 后序遍历右子树
  3. 后序遍历根节点

上面树的访问顺序为：。

4. 层序遍历(Level Order Traversal)

访问顺序：
从上到下从左到右。
上面树的访问顺序为：。

5. 遍历的作用
  1. 前序遍历：树状结构的展示
  2. 中序遍历：二叉搜索树的中序遍历按升序或降序处理节点
  3. 后续遍历：适用于一些先子后父的操作
  4. 层序遍历: 计算二叉树高度，判断二叉树为完全二叉树

4. 二叉搜索树的复杂度分析

如果按照7、4、9、2、5、8、11的顺序添加节点，形成满二叉树如下图

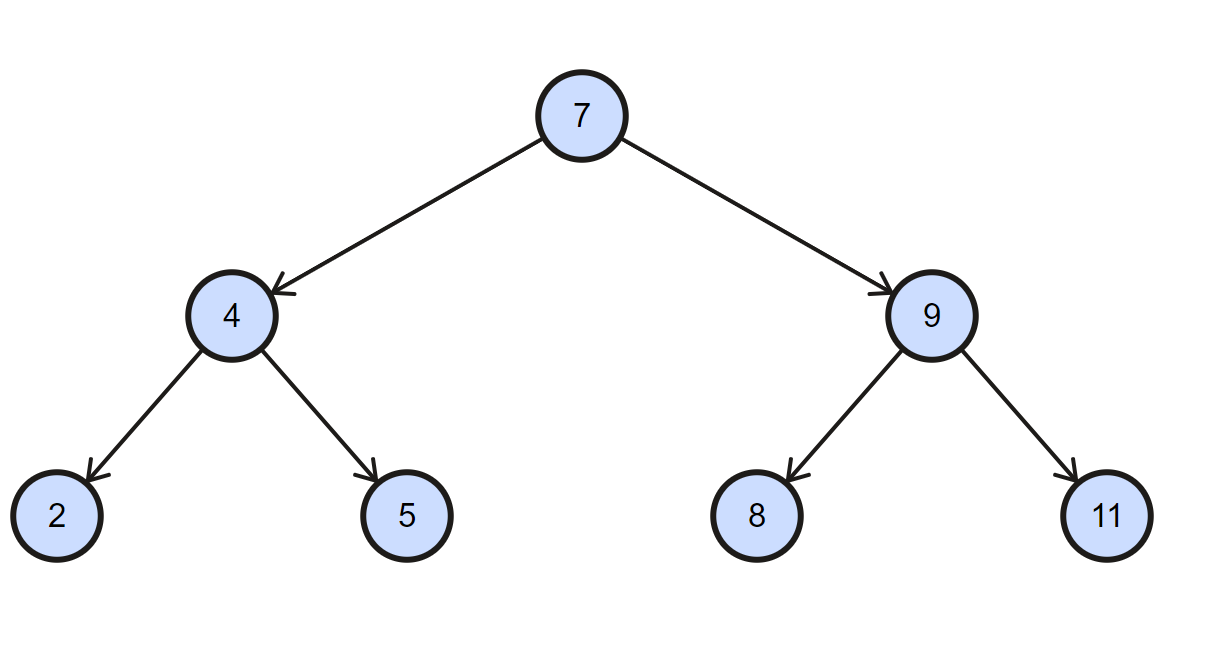
image-20201209205738371

那么搜索，删除，添加复杂度为$O(h)=O(logn)$等于树的高度。

如果按照2、5、4、7、8、9、11添加节点，形成链表：$O(h)=O(n)$。

3. 平衡二叉树

  1. 平衡
    当节点数量固定是，左右子树的高度越接近，这棵树就越平衡。
  2. 理想平衡
    最理想的平衡就是像完全二叉树、满二叉树那样，高度是最小的

1. 平衡二叉搜索树(Balanced Binary Search Tree)

  1. 经典常见的平衡二叉树搜索树有:

    • AVL， Windows NT内核中广泛应用

    • 红黑树：

      • C++ STL中map set

      • Java中TreeMap、TreeSet、HashMap、HashSet

      • Linux的进程调度

2. AVL树

  1. 平衡因子(Balance Factor)：某节点的左右子树的高度差
  1. AVL树的特点:
    • 每个节点的平衡因子只能是1、0、-1(故其绝对值$\le1$，如果超过1，称之为“失衡”)
    • 每个节点的左右子树高度差不超过1
    • 添加、搜索、删除时间复杂度是O(logn)
  2. 最小不平衡树:
    • 距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树，我们称为最小不平衡树。

3. 左单旋 Left Rotation

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

  1. 左旋：将右子树的左子树链接到父节点的右子树节点， 父节点作为新根节点的左子树节点。如下三图所示，

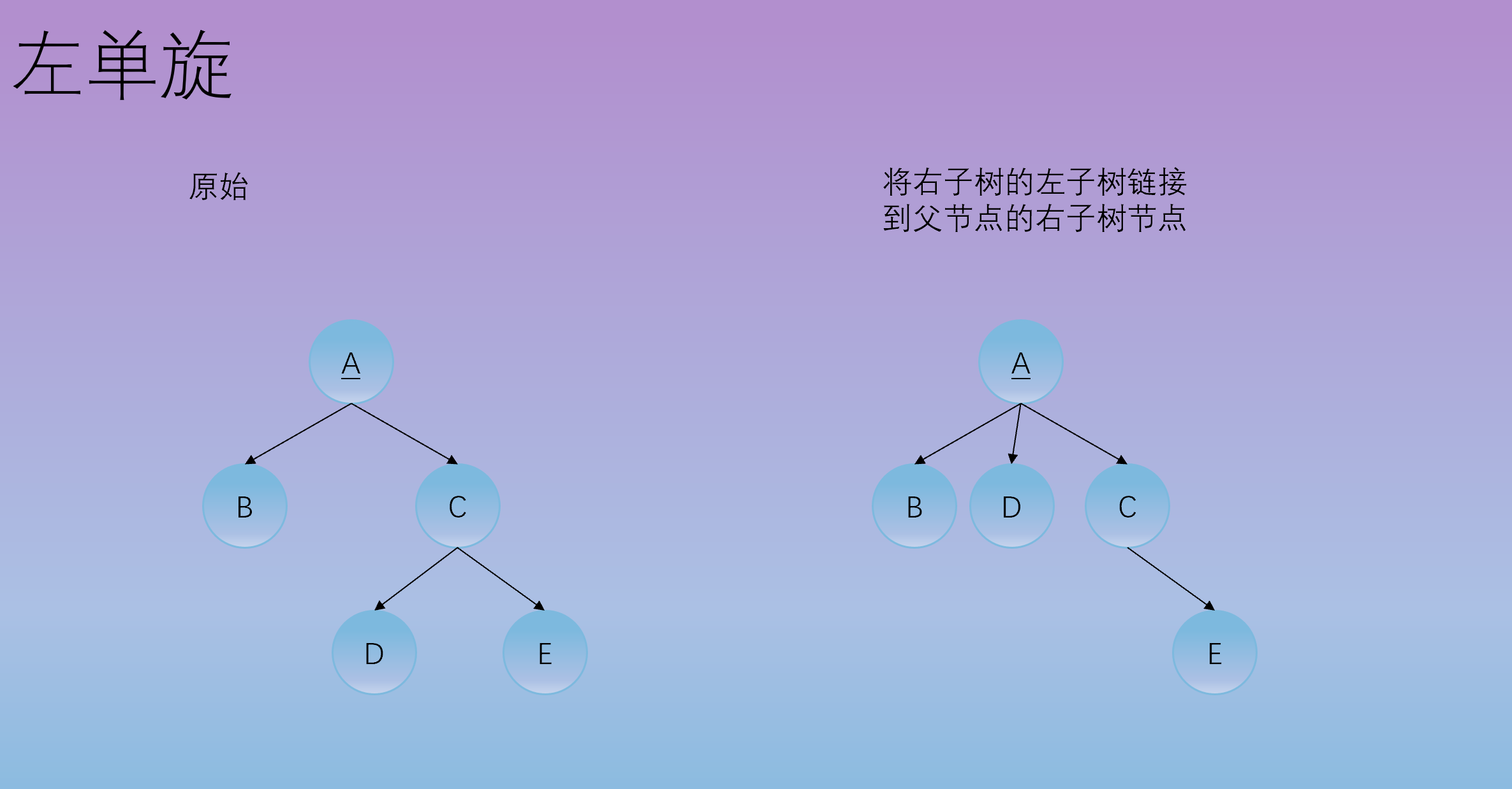
image-20210201122958880

image-20210201123030650

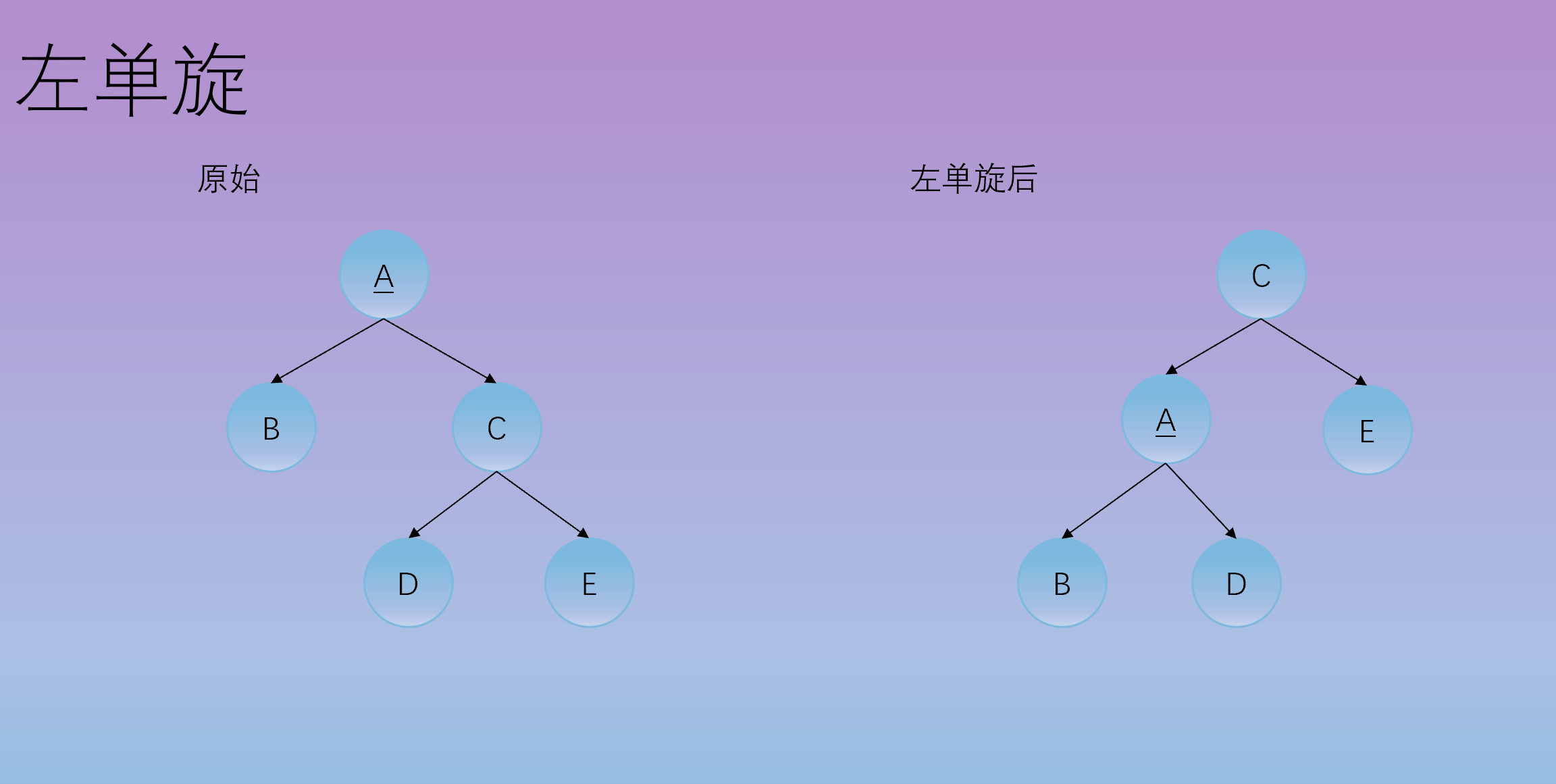
image-20210201123100308

4. 右单旋 Right Rotation

  1. 右旋：右单旋是左单旋的镜像旋转.
    将左子树的右子树链接到父节点的左子树节点，父节点作为新根节点的右子树节点。如下三图所示，

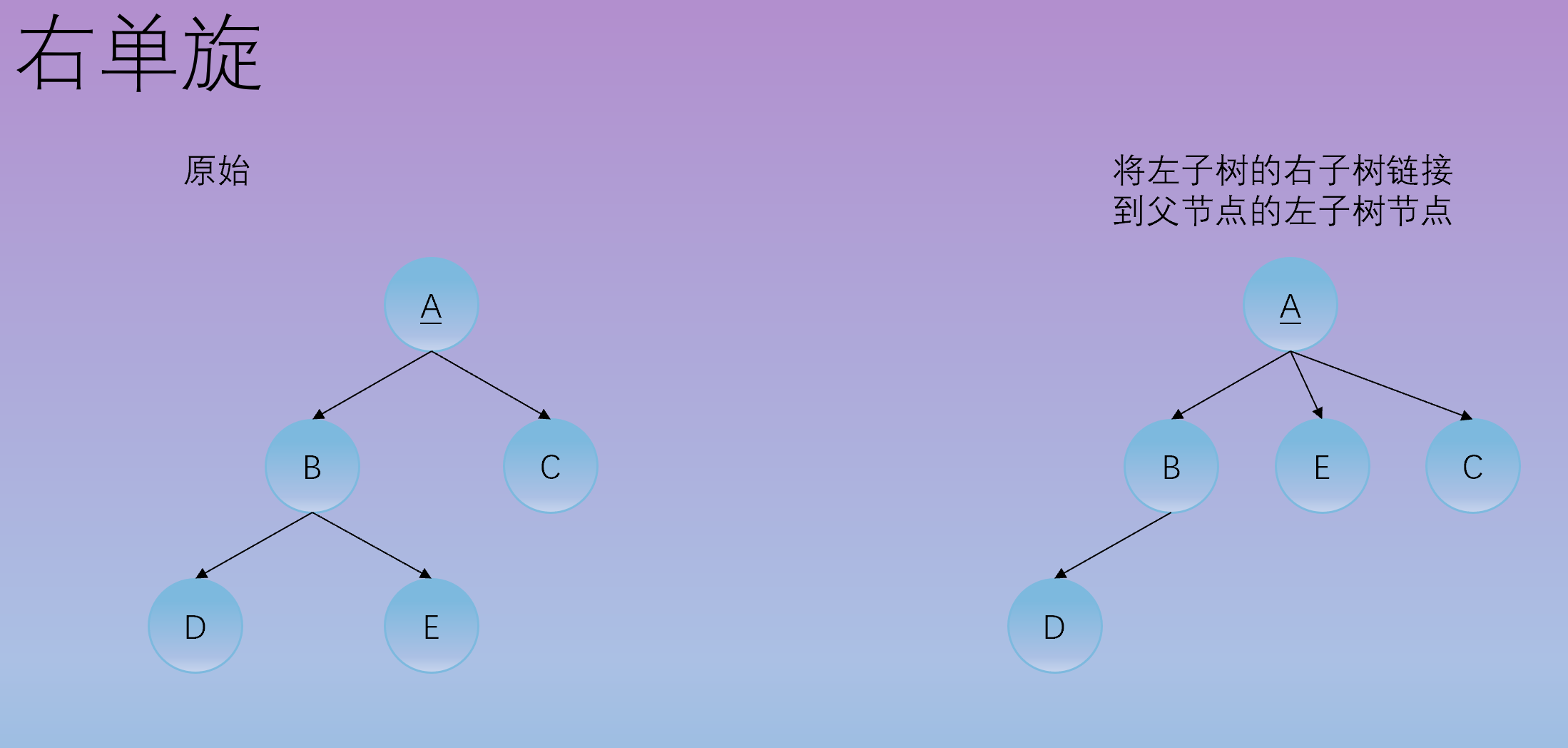
image-20210201123326326

image-20210201123237836

image-20210201123403582

左旋——自己变为右孩子的左孩子；右旋——自己变为左孩子的右孩子

[1] 大话数据结构笔记