1. 集成学习 bagging,boosting和stacking
集成学习 bagging,boosting和stacking
集成学习是通过训练弱干个弱学习器,并通过一定的结合策略,从而形成一个强学习器。有时也被称为多分类器系统(multi-classifier system)、基于委员会的学习(committee-based learning)等。
集成学习先产生一组“个体学习器”(individual learner),再用某种策略将它们结合起来。通常来说,很多现有的学习算法都足以从训练数据中产生一个个体学习器。一般来说,我们会将这种由个体学习器集成的算法分为两类:
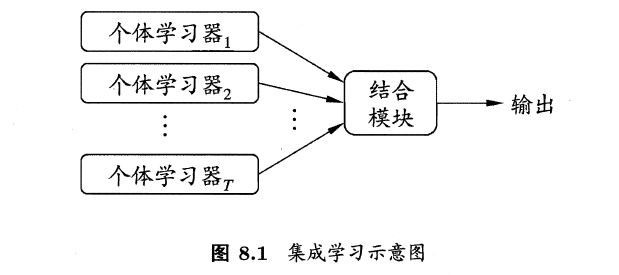
1.同质(homogeneous)的,即集成中仅包含同种类型的一个体学习器,像“决策树集成”中就仅包含决策树,“神经网络集成”中就全是神经网络。同质集成中的个体学习器又称为基学习器(base learner),相应的学习算法也被称为基学习算法(base learning algorithm)。
2.异质(heterogenous)的,相对同质,异质集成中的个体学习其就是由不同的学习算法生成的,这是,个体学习器就被称为组件学习器(component learner)。
其中用的比较多的是同质学习器。同质学习器按照个体学习器之间是否存在依赖关系可以分为两类:
- 第一个是个体学习器之间存在强依赖关系,一系列个体学习器基本都需要串行生成,代表算法是boosting系列算法;
- 第二个是个体学习器之间不存在强依赖关系,一系列个体学习器可以并行生成,代表算法是bagging和随机森林(Random Forest)系列算法。
随机森林:
- 样本随机:从数据集中用bagging方式随机选取n个样本
- 特征随机:从所有特征d中随机选择k个属性(k<d),然后从k个属性中选取最佳分割属性作为节点建立CART决策树
- 重复1.2步m次建立m棵CART树
- 这m棵CART树形成随机森林,通过投票表决决定输入属于哪一类。
所以说:RF = 决策树 + bagging + 随机特征选取
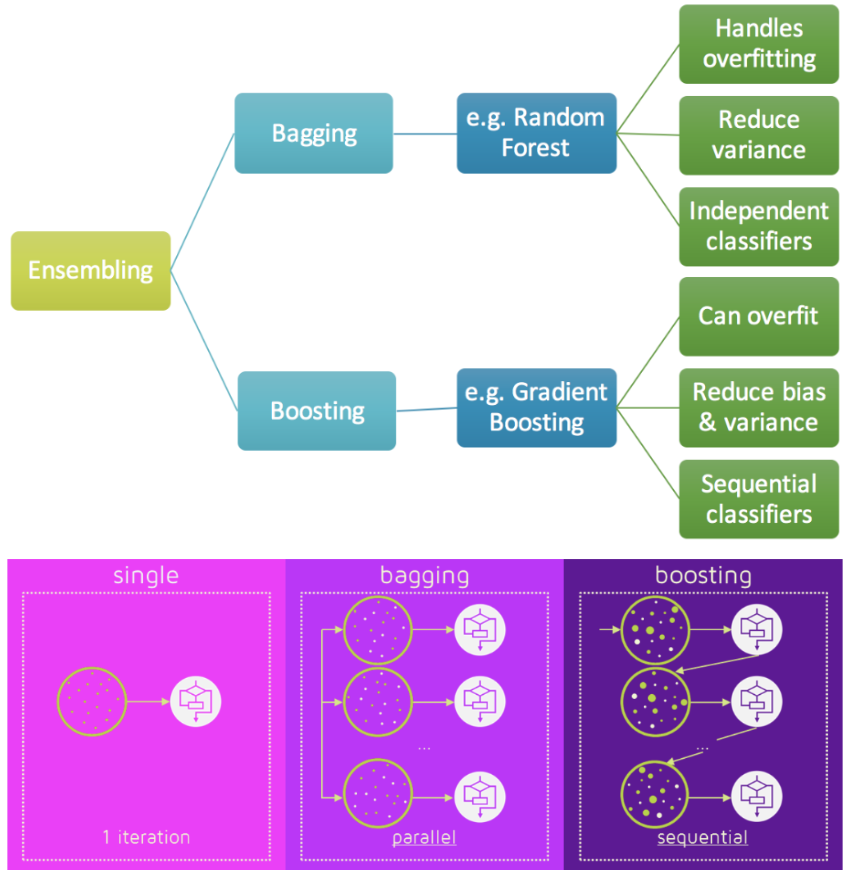
目前,有三种常见的集成学习框架:bagging,boosting和stacking。
1. Bagging
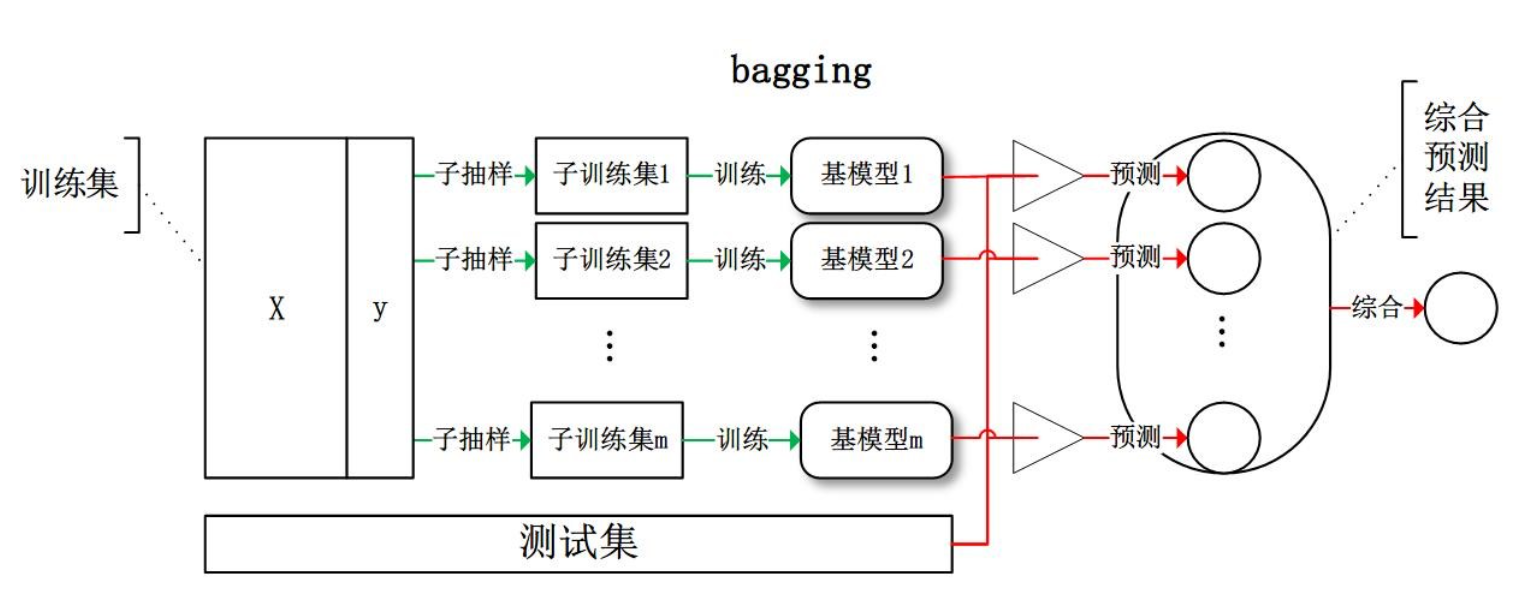
bagging: 从训练集从进行子抽样组成每个基模型所需要的子训练集,对所有基模型预测的结果进行综合产生最终的预测结果。
- 如果是回归任务,bagging 输出是各个弱评估器输出的平均值;
如果是分类任务,bagging 输出是各个弱评估器输出的结果的少数服从多数voting。
2. Boosting
boosting:
先从初始训练集中训练一个基学习器,再根据基学习器的表现对训练样本进行调整,使得先前基学习器预测错误的训练样本受到更多关注,然后基于调整后的样本分布训练下一个基学习器;如此重复进行,直到基学习器达到事先指定的值T, 最终将T个基学习器进行加权结合输出预测值。
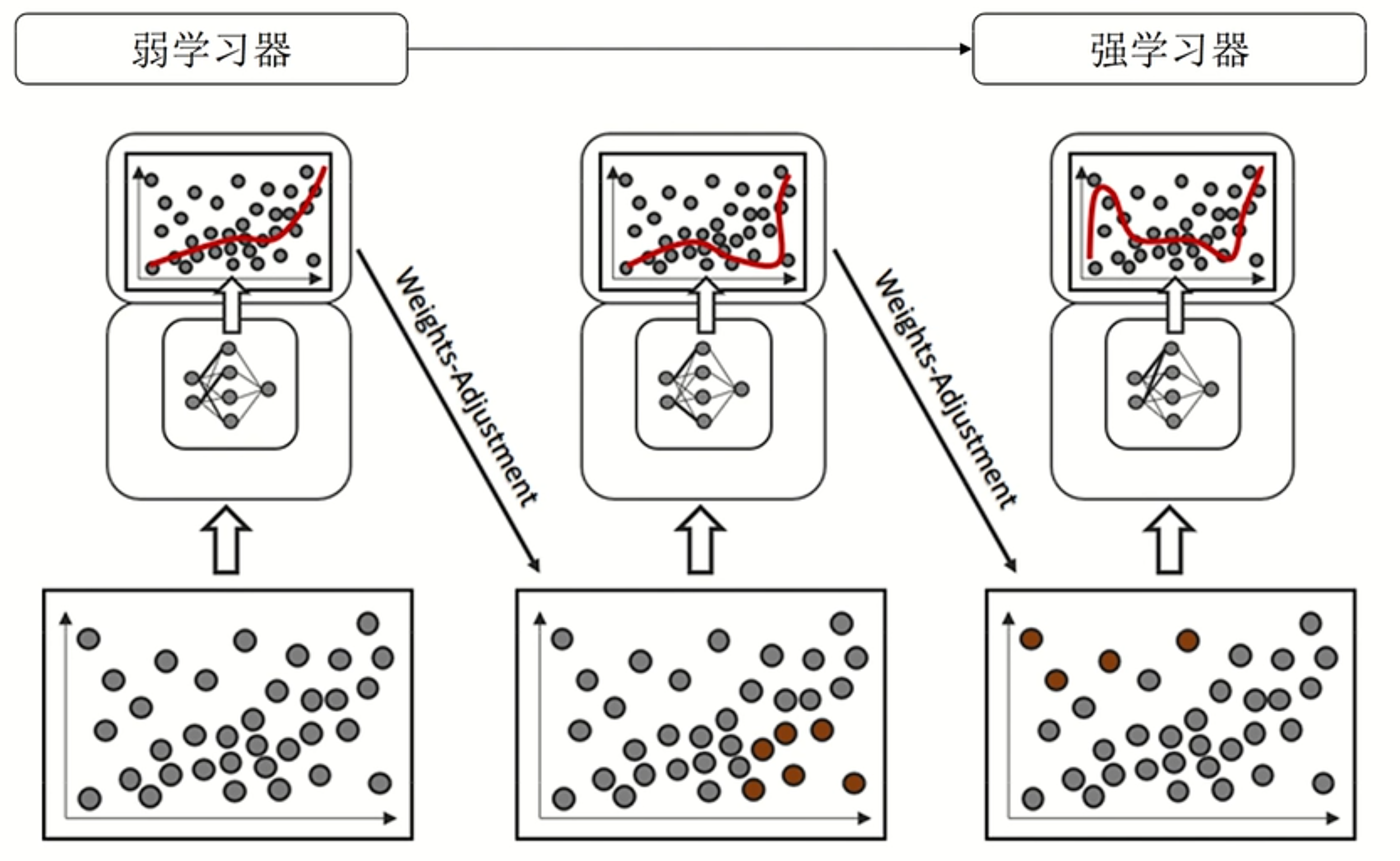
bagging vs boosting:
| 装袋法 Bagging | 提升法 Boosting | |
|---|---|---|
| 弱评估器 | 相互独立,并行构建 | 相互关联,按顺序依次构建。 先建弱分类器的预测效果影响后续模型的建立 |
| 建树前的抽样方式 | 样本有放回抽样 特征无放回抽样 |
样本有放回抽样(后面步骤抽样权重不一样) 特征无放回抽样 先建弱分类器的预测效果可能影响抽样细节 |
| 集成的结果 | 回归平均 分类投票 |
每个算法具有自己独特的规则,一般来说: (1)表现为某种分数的加权平均 (2)使用输出函数 |
| 目标 | 降低方差 提高模型整体的稳定性来提升泛化能力 本质是从“平均”这一数学行为中获利 |
降低偏差 提高模型整体的精确度来提升泛化能力 从众多弱分类器叠加后可以等同于强学习器 |
| 单个评估器容易过拟合的时候 | 具有一定的抗过拟合能力 | 具有一定的抗过拟合能力 |
| 单个评估器的效果比较弱的时候 | 可能失效 | 大概率会提升模型表现 |
| 代表算法 | 随机森林 | 梯度提升树GBDT,Adaboost |
Boosting 代表算法 Adaboost
Adaboost算法流程如下(来自于周志华《机器学习》P174)。

这里定义的是简单的二分类数据任务,其中:
- : 表示数据集,后面的表示第轮重新划分后的数据集。
- : 表示第轮基模型
- : 表示第轮错误率
- : 可理解为真实值
- :权重,是最后用来对各个基学习器加权的权重
- : 表示第轮归一化因子
有了以上定义,我们来看看整个算法的流程:给定的训练集,使用基学习算法,训练轮。图示步骤解释,给个具体计算例子:
- 对于第一轮,基于每个样本一个相等的权重
- 从第1轮到到第T轮做步骤3-7
- 用基学习算法,如决策树,对第轮数据集进行学习得到
- 计算第轮获得的对样本错误率
- 如果错误率大于0.5,直接break(二分类)
- 计算权重,因为,而。所以中ln内部是大于等于1的,那么。并且对于升高,是下降的。
- 这里,如果分类正确,那么错误率高,而是下降的,用来计算相对是下降的。反之亦然。这样符合错误分类样本权重增加,正确分类样本权重下降的原则。
一般表达:
- 首先,是初始化训练数据的权值分布D1。假设有N个训练样本数据,则每一个训练样本最开始时,都被赋予相同的权值:w1=1/N。
- 然后,训练弱分类器。具体训练过程中是:如果某个训练样本点,被弱分类器准确地分类,那么在构造下一个训练集中,它对应的权值要减小;相反,如果某个训练样本点被错误分类,那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 最后,将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
- 换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
利用sklearn实现简单的adaboost代码:
1 | from sklearn.ensemble import AdaBoostClassifier # For Classification |
- learning_rate: 控制在最后的组合中每个弱分类器的权重,需要在learning_rate和n_estimators间有个权衡。
至于GBDT算法,可以看GBDT部分.
3.Stacking
stacking:先从初始训练集中训练一个初级学习器,然后将样本输入得到,将构建新的数据集,继续训练得到新的学习器。但这样直接用初级学习器的训练集作为输入,得到新的训练集很容易过拟合。因此一般用Kfold划分初始训练集,用留出法得到留出的那一个fold数据集来得到下一级训练集。
具体算法流程如下,西瓜书P184。

步骤1-3 是训练出来个体学习器,也就是初级学习器。
步骤5-9是 使用训练出来的个体学习器来得预测的结果,这个预测的结果当做次级学习器的训练集。
步骤11 是用初级学习器预测的结果训练出次级学习器,得到我们最后训练的模型。
如果想要预测一个数据的输出,只需要把这条数据用初级学习器预测,然后将预测后的结果用次级学习器预测便可。


