CS224N Lecture 6 Vanishing Gradients, Fancy RNNs, Seq2Seq
The Simple RNN Language Model
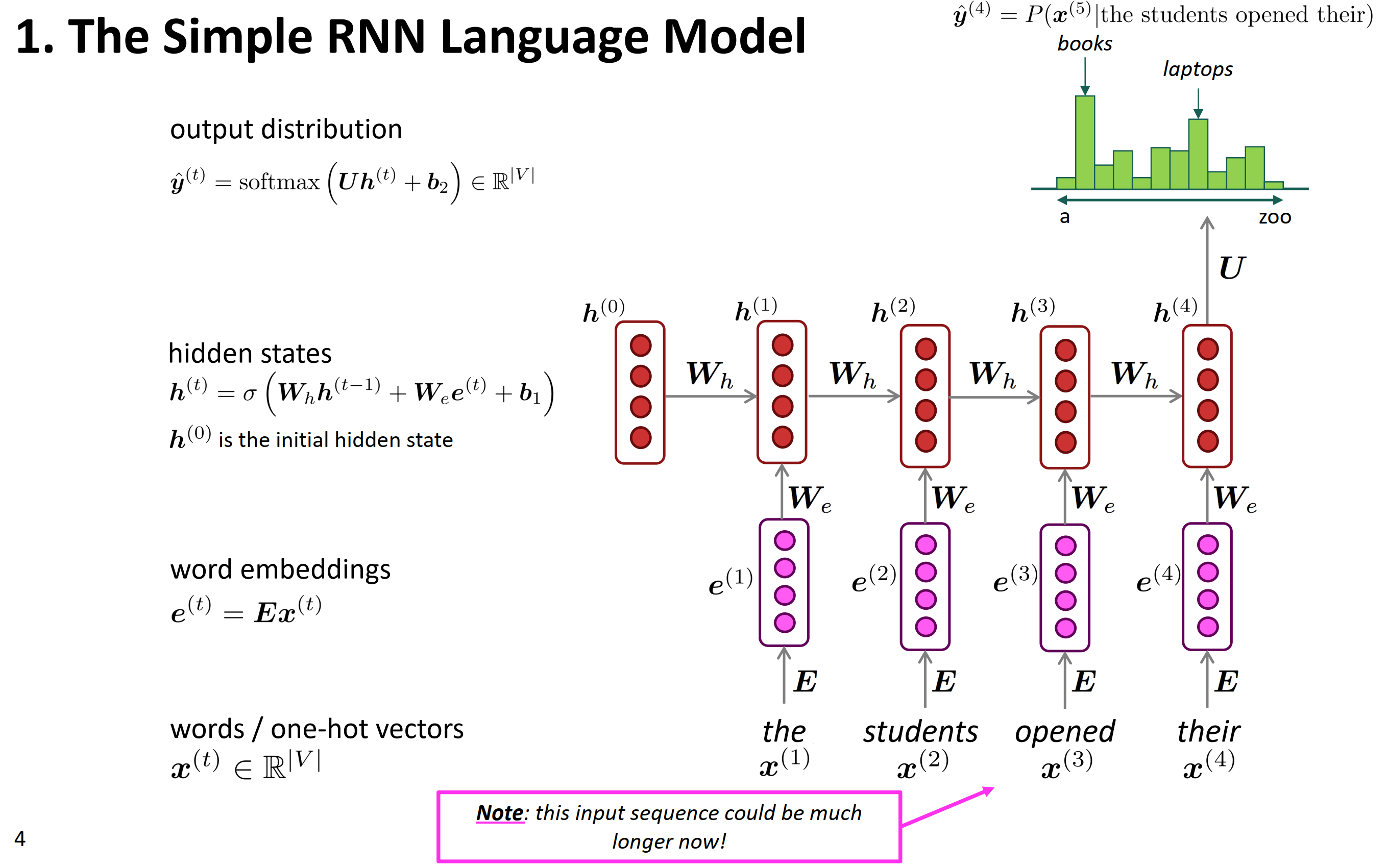
简单的RNN语言模型。
Training an RNN Language Model

RNN在$t$时刻的输出是预测第$t+1$个词的概率分布$y^(t)$;而对于训练集中给定的文本来说,第$t+1$个词是已知的某个词,所以真实答案$y(t)$其实是一个one-hot向量,在第$x(t+1)$位置为1,其他位置为0。所以如果是交叉熵损失函数的话,表达式如上图中间的等式。RNN整体的损失就是所有时刻的损失均值。
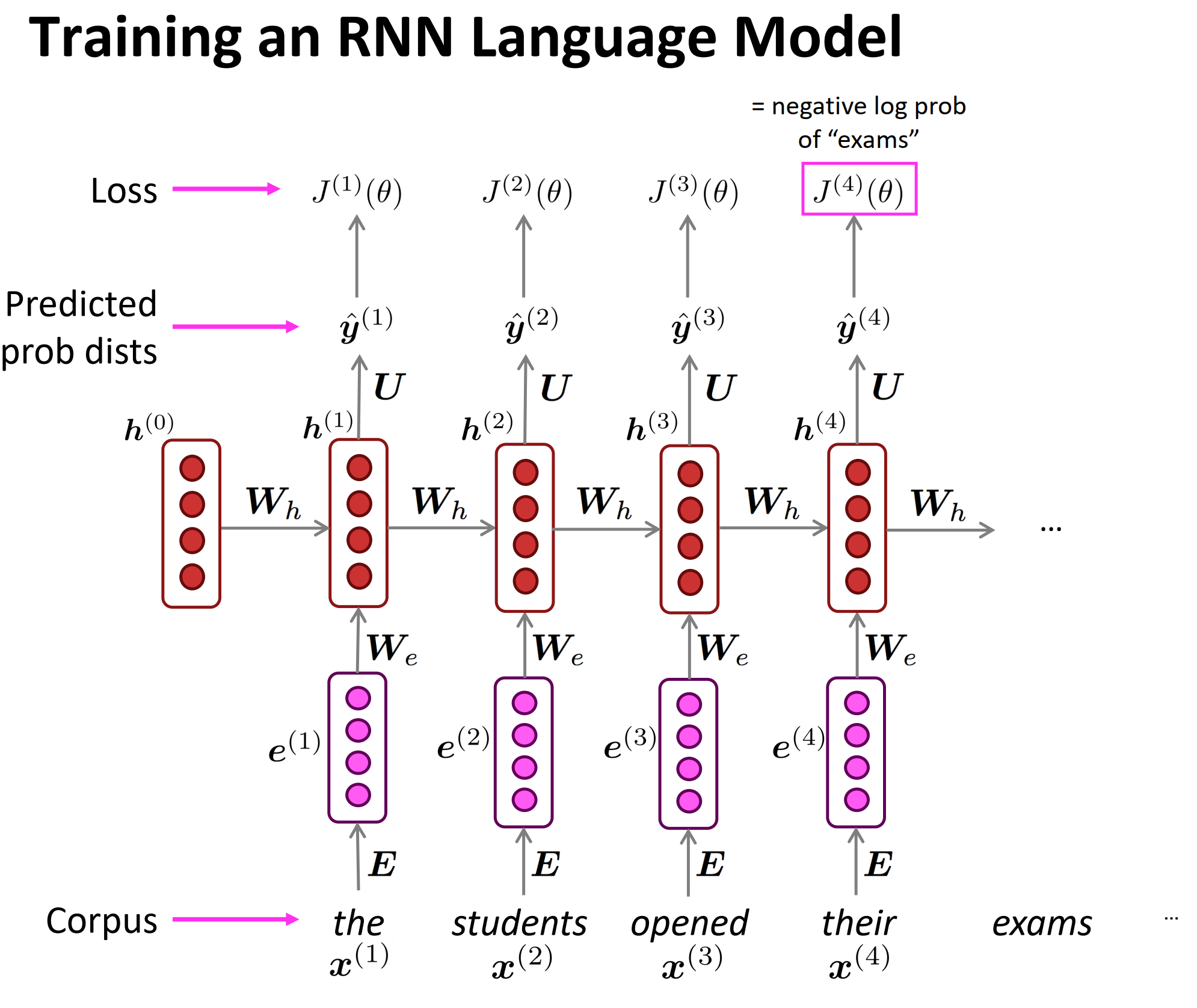
输入序列the students opened their 预测后面的词。
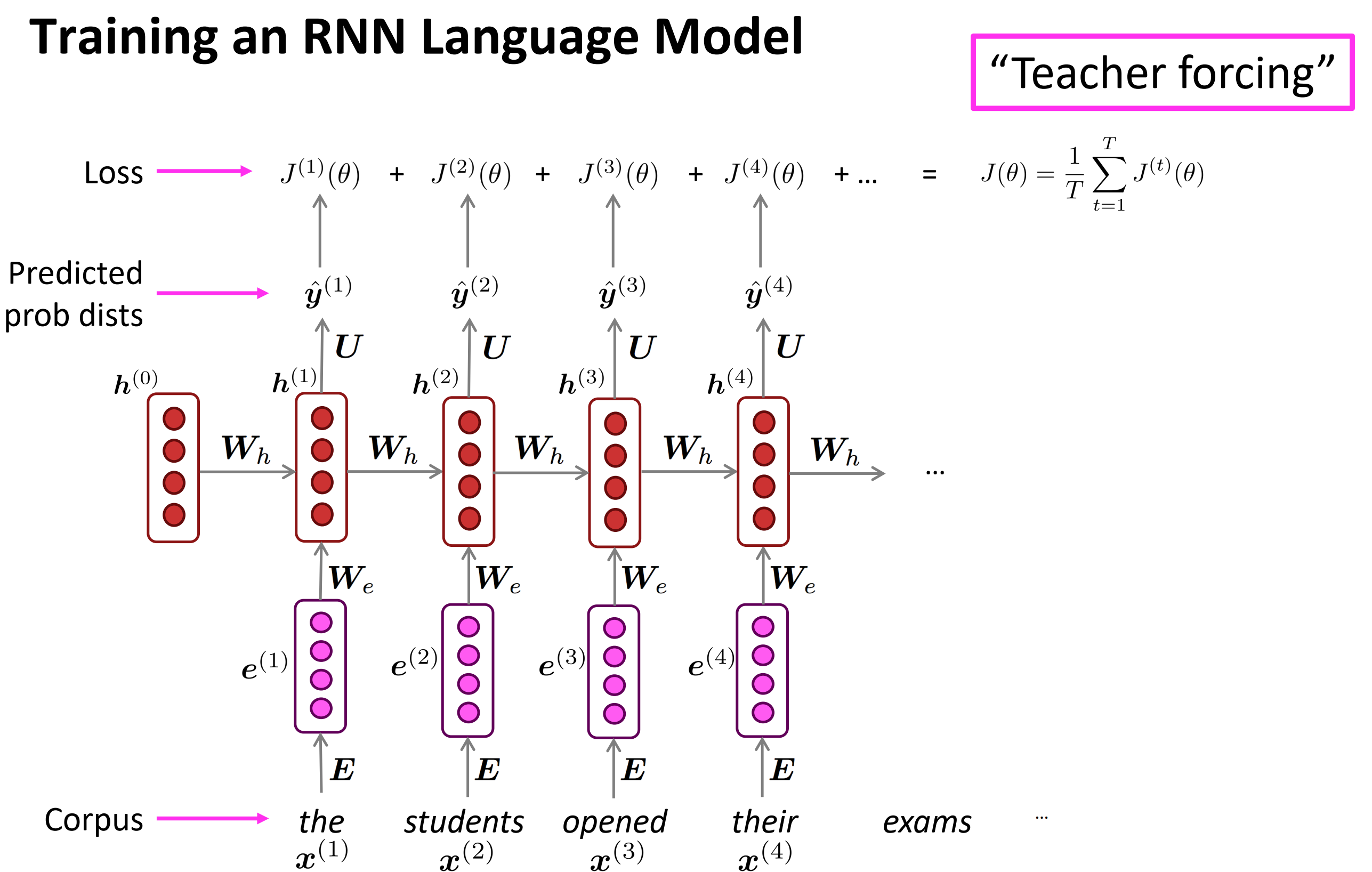
训练RNN语言模型,其实loss是所有时刻t的损失的均值。

然而:计算 整个语料库 的损失和梯度太昂贵了
在实践中,输入序列实际上是一个 句子 或是 文档,这就跟随机梯度下降法中,随机抽小批样本一样。
- 回忆 :随机梯度下降允许我们计算小块数据的损失和梯度,并进行更新。
- 计算一个句子的损失(实际上是一批句子),计算梯度和更新权重。重复上述操作。
Training the parameters of RNNs: Backpropagation for RNNs
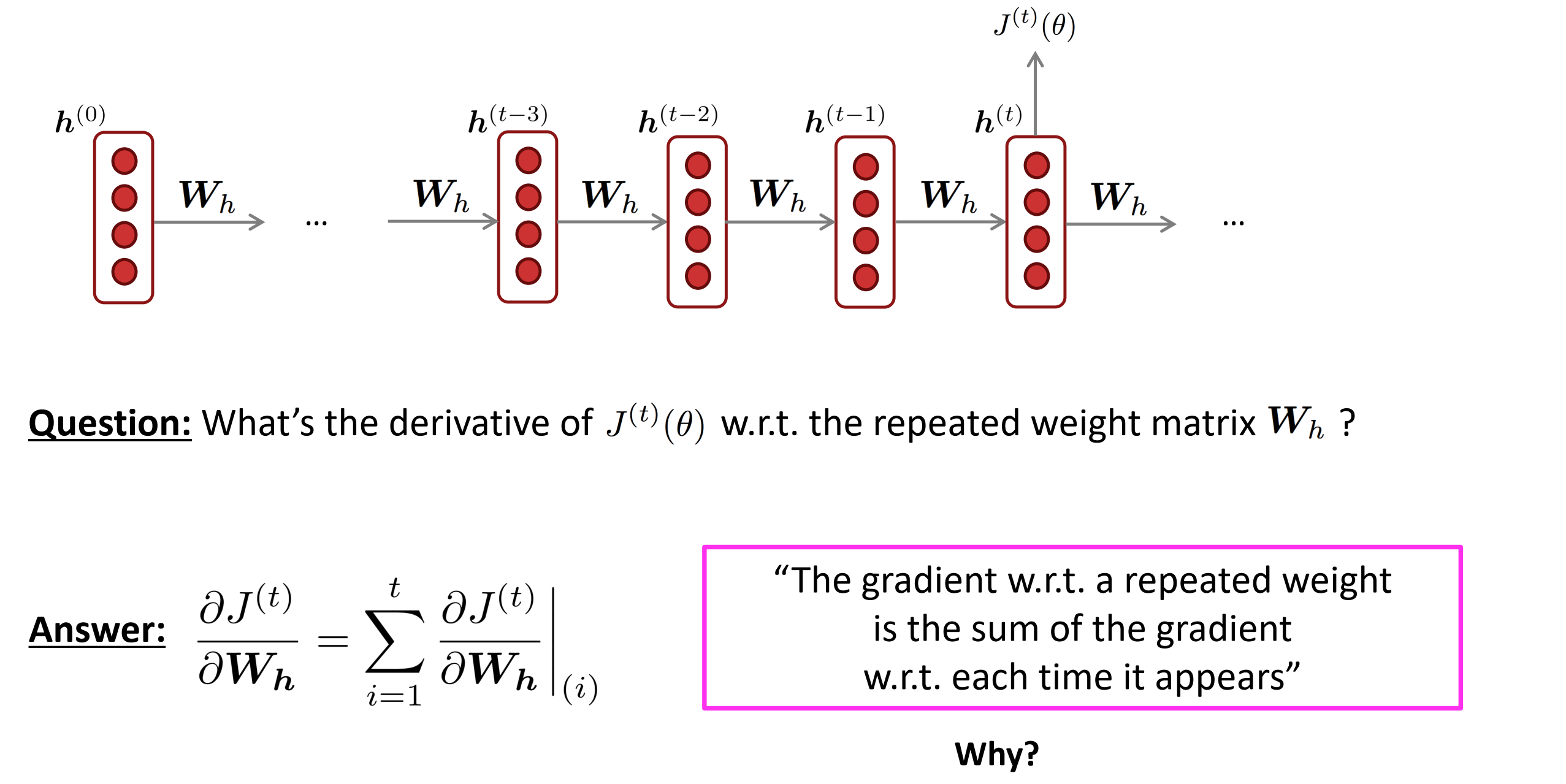
损失函数对权重矩阵W等参数的偏导是什么?
Problems with Vanishing and Exploding Gradients
Vanishing gradient intuition
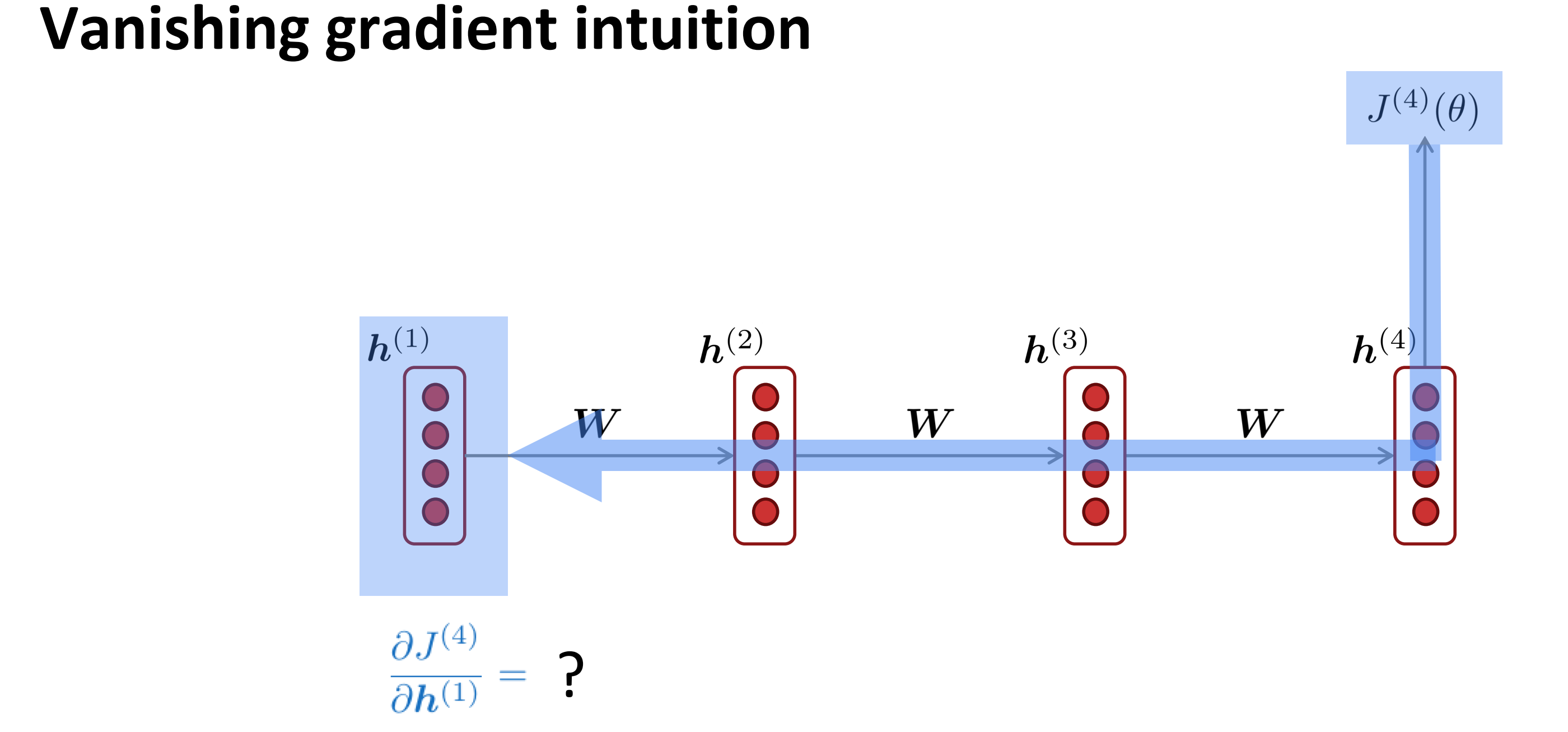
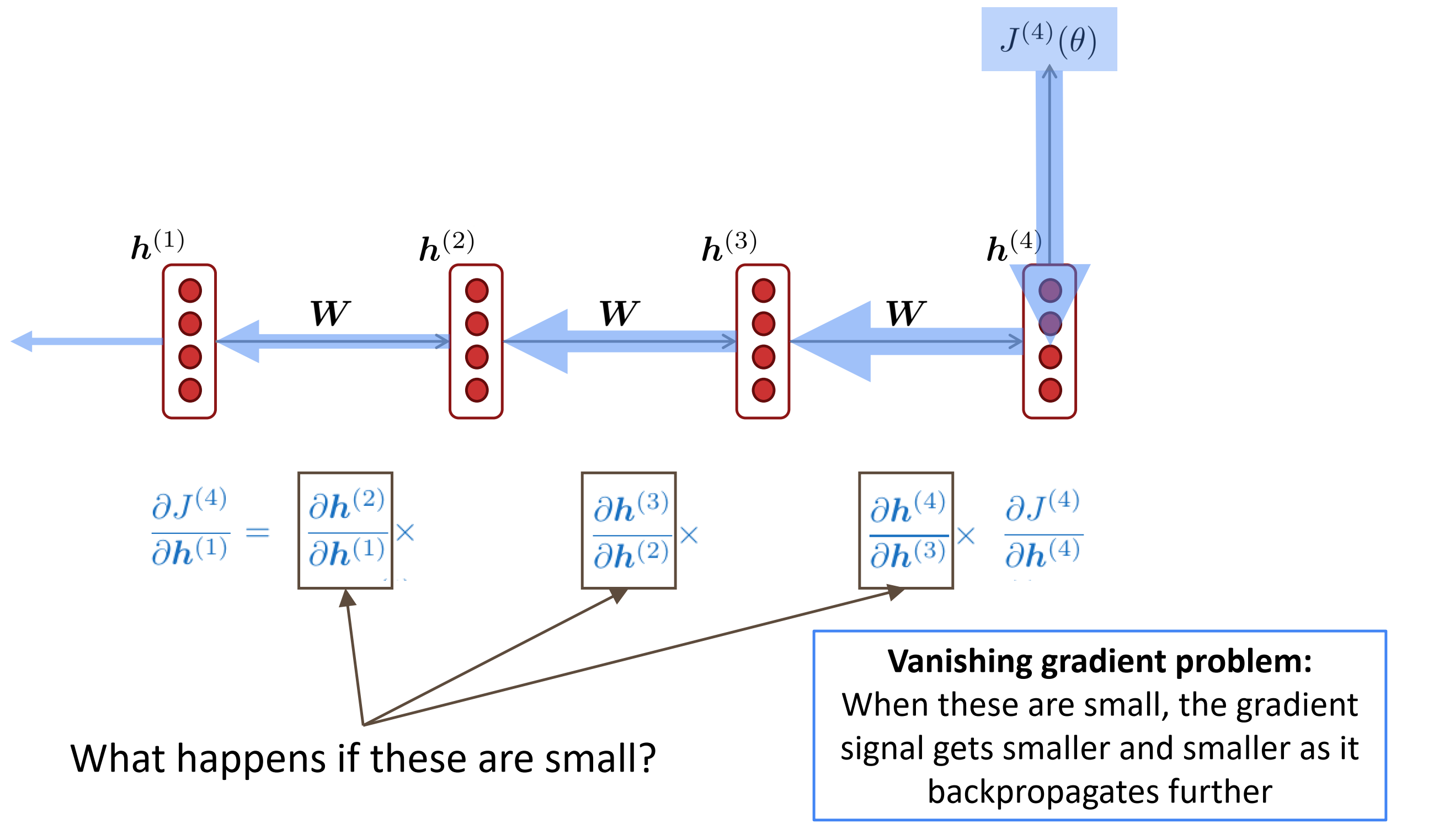
梯度消失的直觉,根据链式法则,求每个节点对隐藏变量$\mathbf{h}_i$的梯度时,如果其接近0时,传播越深,梯度信号就会越来越小,直至消失。
Vanishing gradient proof sketch (linear case)

对于隐藏层$\mathbf{h}^{(t)}$来说,就是激活函数作用到,上一个隐藏输入和输入分布的权重和加上偏置。
如果激活函数是恒等函数,比如$\sigma(x) = x$,
其梯度就是上面的整体的导数的对角阵再乘以 ;即单位矩阵乘以考虑第$i$时刻损失 对于在之前时刻 隐藏层 的梯度,令
如果$\mathbf{W}_{h}$本身非常小,当$l$变大时,这项会产生指数问题。

- $\mathbf{W}_{h}^{l}$什么问题?
- 假设$\mathbf{W}_{h}$的特征值都小于1:
- 可以将其梯度写作$\mathbf{W}_{h}$的一组基的形式,这时,就会导致梯度消失
- 那非线性激活函数$\sigma$呢?也一样,除了需要证明对于在维度上一些$\gamma$独立和$\sigma$有$\lambda_i < \gamma$
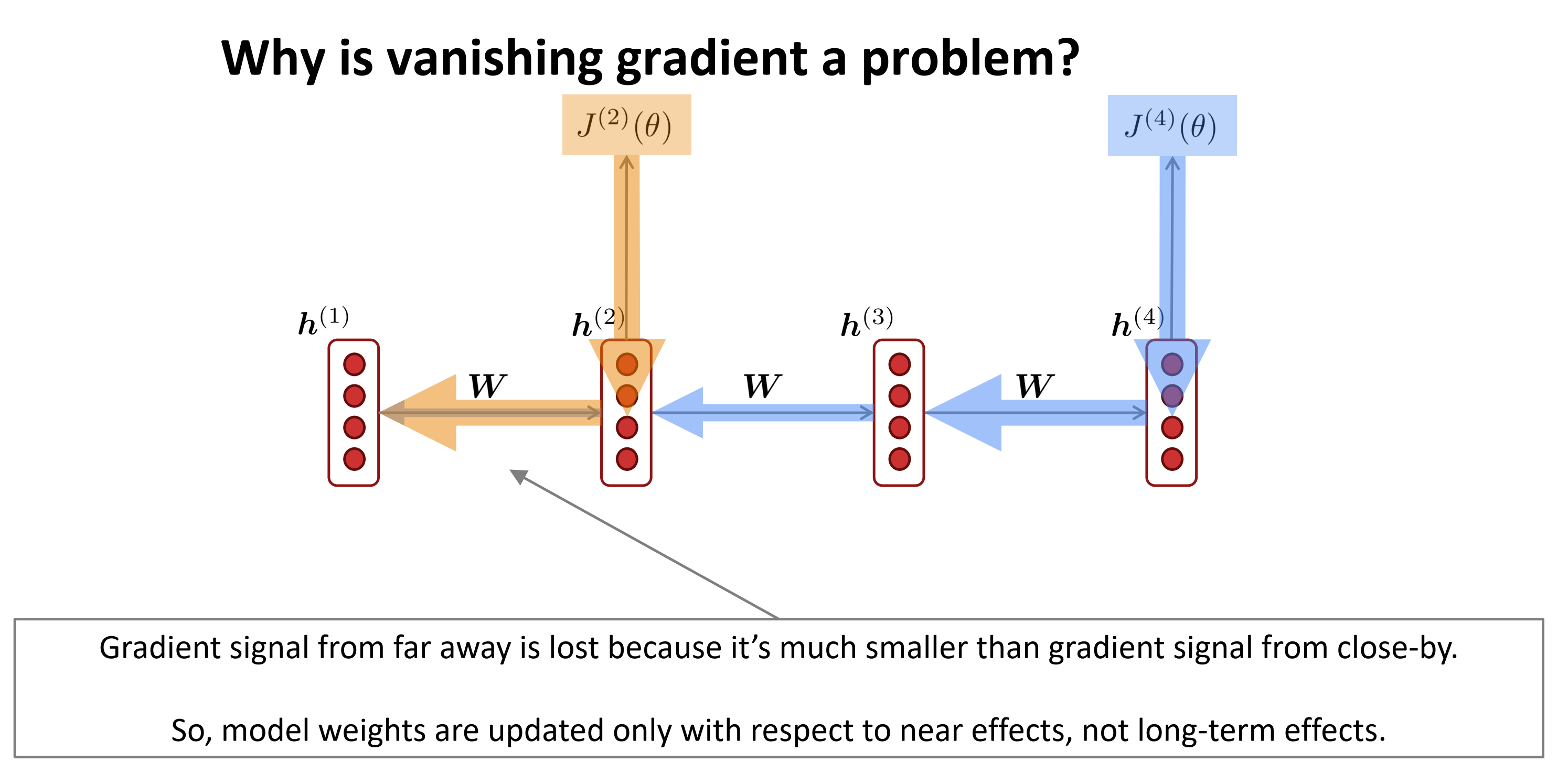
为什么梯度消失是一个问题?
- 梯度信号从远处传来会消失是因为,它比近处的小得多
- 因此,模型权重只会更新对应的近处影响,而不是长期的影响
Effect of vanishing gradient on RNN-LM

- 语言模型的任务:预测下一个词
- 为了从训练样本学习到这个,语言模型需要建立依赖于在第7步“tickets” 和最后目标词“tickets”之间的的模型。
- 但是如果梯度很小,模型就无法学习到这个依赖关系。因此模型无法在测试时预测类似的长距离依赖关系
Why is exploding gradient a problem?

- 如果梯度变得过大,那么SGD更新步伐将变大
这将导致错误的更新:我们取太大的步伐,到达一个怪异的错误的参数配置(产生大的loss)
- 你想下你发现一个斜坡来跳跃,但突然你在低谷了
在最坏的情况下,这会在你网络中导致NaN(那么你得从之前某个checkpoint重新训练)
Gradient clipping: solution for exploding gradient
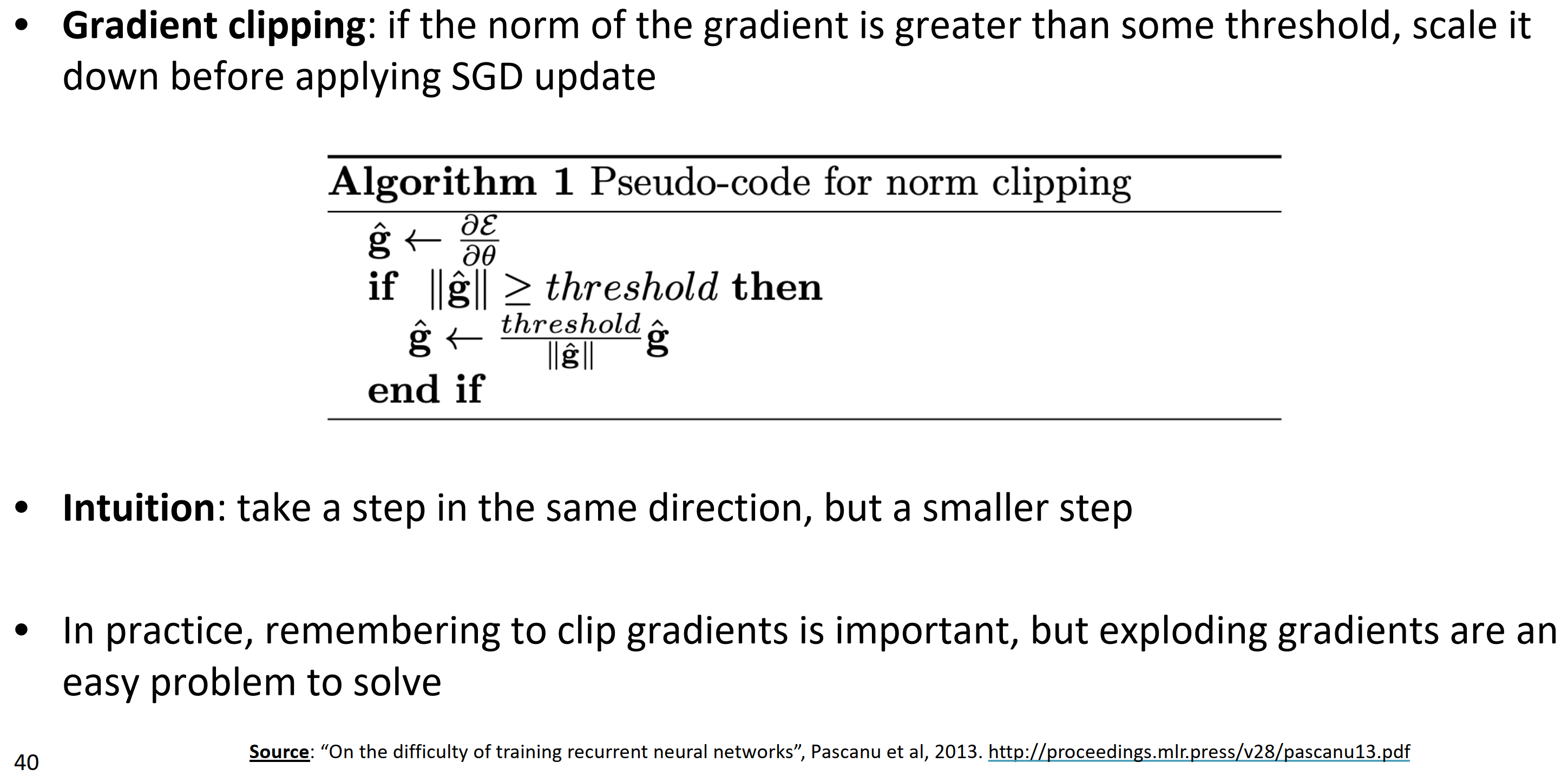
- 梯度裁剪:就像算法1中,如果梯度的模大于阈值,就在SGD之前缩小它
- 直觉:取同样方向的一步,不过是一小步
- 实际上,记得裁剪梯度是非常重要的,但梯度爆炸是一个容易解决的问题。
How to fix the vanishing gradient problem?

主要问题是在,对于RNN很难学到遍历许多时刻后保留信息
在RNN变种里,隐藏状态不断被重写
RNN有独立记忆怎么样?
引入LSTM
Long Short-Term Memory RNNs (LSTMs)

在1997年一种类型的RNN被Hochreiter and Schmidhuber 提出,其作为梯度消失问题的解决措施。
- 每个人引用这篇论文,但是现代LSTM真正关键部分源自Gers Learning to Forget: Continual Prediction with LSTM
在时刻$t$, 有一个隐藏状态$\mathbf{h}^{(t)}$和cell状态$\mathbf{c}^{(t)}$
- 都是长度为$n$的向量
- cell存储长期信息
- LSTM能从cell中读取、删除,和写入信息 ,cell是一个概念而不是计算机里的RAM
- 通过控制三个对应的门来删除、写入、读取选择性的信息
- 门也是长为$n$的向量
- 在每个时刻,每个门元素能打开(1), 关闭(0),或者介于之间状态
- 门是动态的:基于当前上下文来计算它们的值
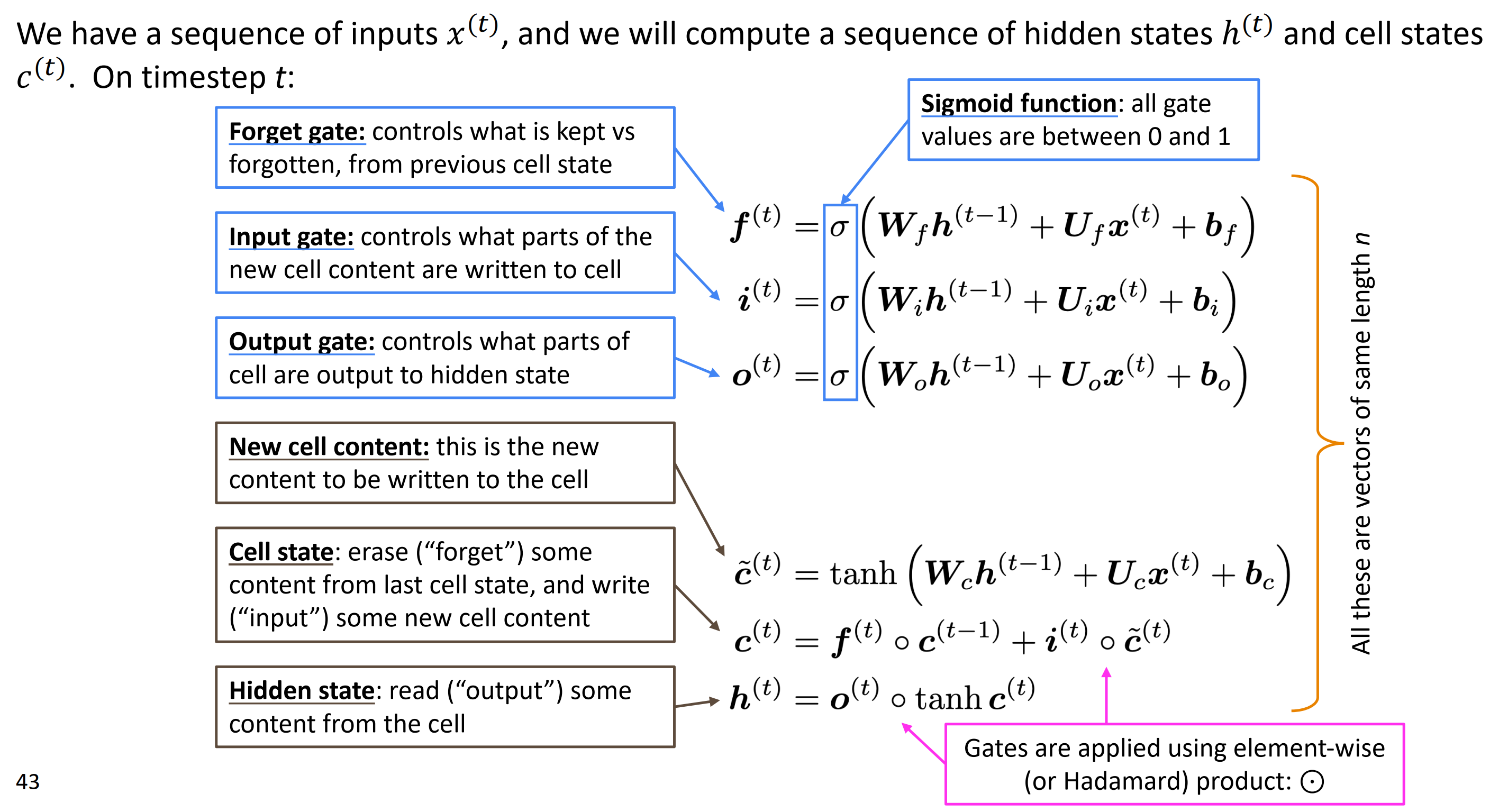
我们有一个输入序列$\mathbf{x}^{(t)}$,要计算隐藏状态$\mathbf{h}^{(t)}$序列和cell状态$\mathbf{c}^{(t)}$.在时刻$t$:
- 遗忘门:控制上一个cell状态的保持和遗忘,$\mathbf{f}^{(t)}=\sigma(\mathbf{W}_f\mathbf{h}^{(t-1)}+\mathbf{U}_f\mathbf{x}^{(t)} + \mathbf{b}_f)$
- 输入门:控制新cell的哪些内容写入到cell, $\mathbf{i}^{(t)}=\sigma(\mathbf{W}_i\mathbf{h}^{(t-1)}+\mathbf{U}_i\mathbf{x}^{(t)} + \mathbf{b}_i)$
- 输出门:控制哪些cell的部分输出到隐藏层, $\mathbf{o}^{(t)}=\sigma(\mathbf{W}_o\mathbf{h}^{(t-1)}+\mathbf{U}_o\mathbf{x}^{(t)} + \mathbf{b}_o)$
- 新cell内容:写入cell的新内容: $\mathbf{\tilde c}^{(t)}=\text{tanh}(\mathbf{W}_c\mathbf{h}^{(t-1)}+\mathbf{U}_c\mathbf{x}^{(t)} + \mathbf{b}_c)$
- Cell状态: 删除上一个cell“forget”中一些内容,写入“input”一些新cell内容:$\mathbf{c}^{(t)}=\mathbf{f}^{(t)}\circ \mathbf{c}^{(t-1)}+\mathbf{i}^{(t)}\circ \mathbf{\tilde c}^{(t)}$
- 隐藏状态:读取从cell中“输出”一些内容:$\mathbf{h}^{(t)}=\mathbf{o}^{(t)}\circ \text{tanh} \mathbf{c}^{(t)}$
注意:门都是应用的逐元素积或者说Hadamard积。
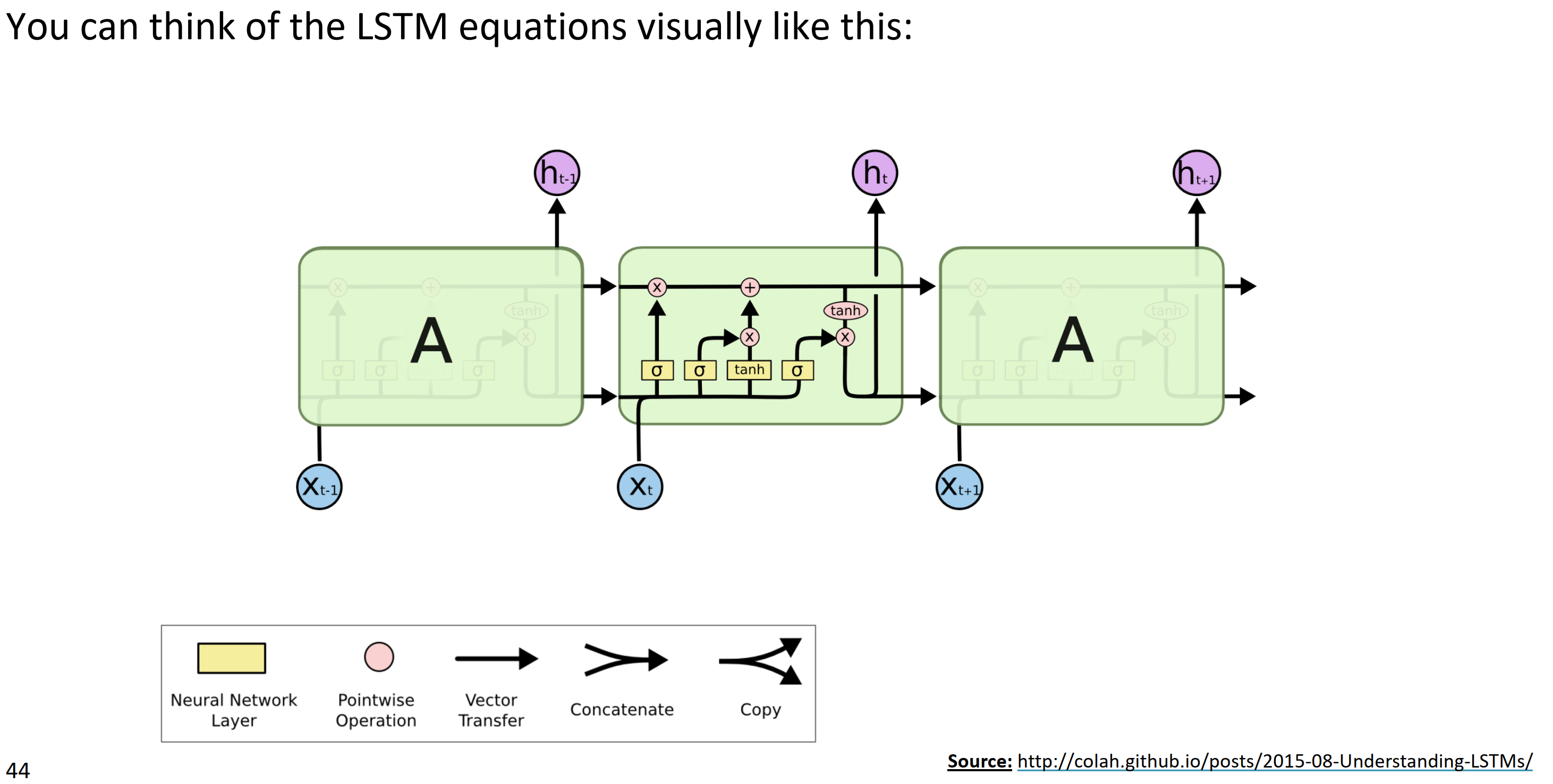
你可以把LSTM方程可视像上图一样, colah LSTM
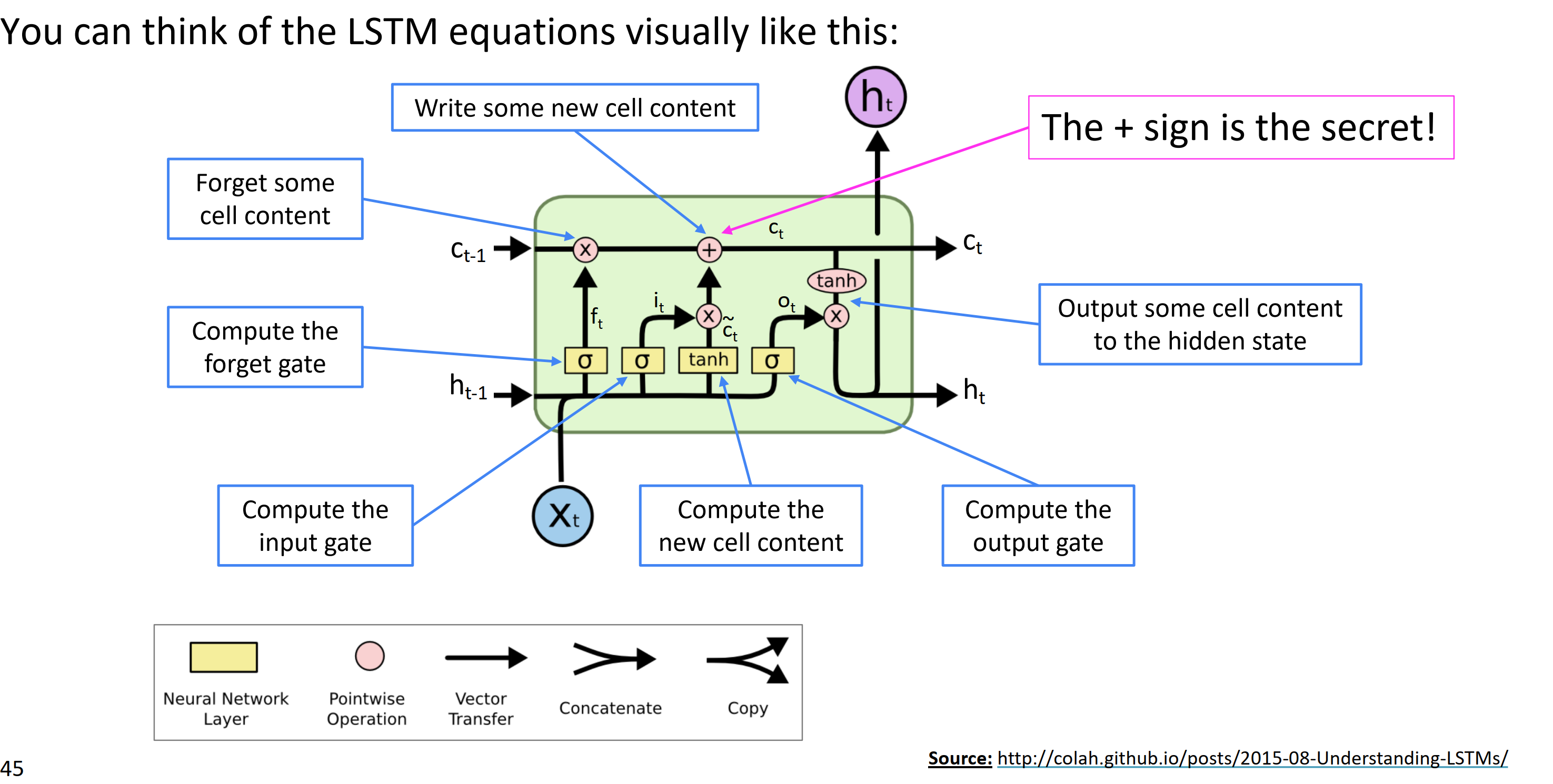
具体来说,来看每个门的作用。
How does LSTM solve vanishing gradients?

LSTM怎么解决梯度消失问题?
- LSTM比RNN更容易保留许多时刻后的信息。
- 比如,如果对于一个cell ,遗忘门设置为1,输入门设置为0,那么这个cell的信息被无限地保留
- 相比,普通RNN很难学到循环权重矩阵$\mathbf{W}_h$, 其保留在隐藏层state的信息
- 实际上,你能得到大约100个时刻而不是7个时刻
- LSTM不确保,没有梯度消失,但是提供了让模型更容易学习长矩依赖的方式
LSTMs: real-world success

LSTM:现实的成功
- 在2013——2015,LSTMs开始取得最先进的成果:
- 成功的任务包含,手写识别,语音识别,机翻,解析,和图片标题,以及语言模型
- LSTM成为大部分NLP任务的统治方法
- 在2021年,别的方法(如Transformers)已经成为许多任务的统治方法
- 例如,在WMT
- 2016 WMT,总结报告包含 “RNN” 44次
- 2019 WMT , “RNN” 7 次, “Transformer” 105次
Is vanishing/exploding gradient just a RNN problem?
梯度消失/爆炸仅仅是RNN中的问题吗?
不是!所有的神经网络(包括前馈和卷积网络)都会存在梯度爆炸或是梯度消失的问题,特别是很深的网络。
- 由于链式法则/非线性激活函数的选择,梯度当其反向传播是渐渐变小
- 因此,低层学习得十分缓慢(很难训练)
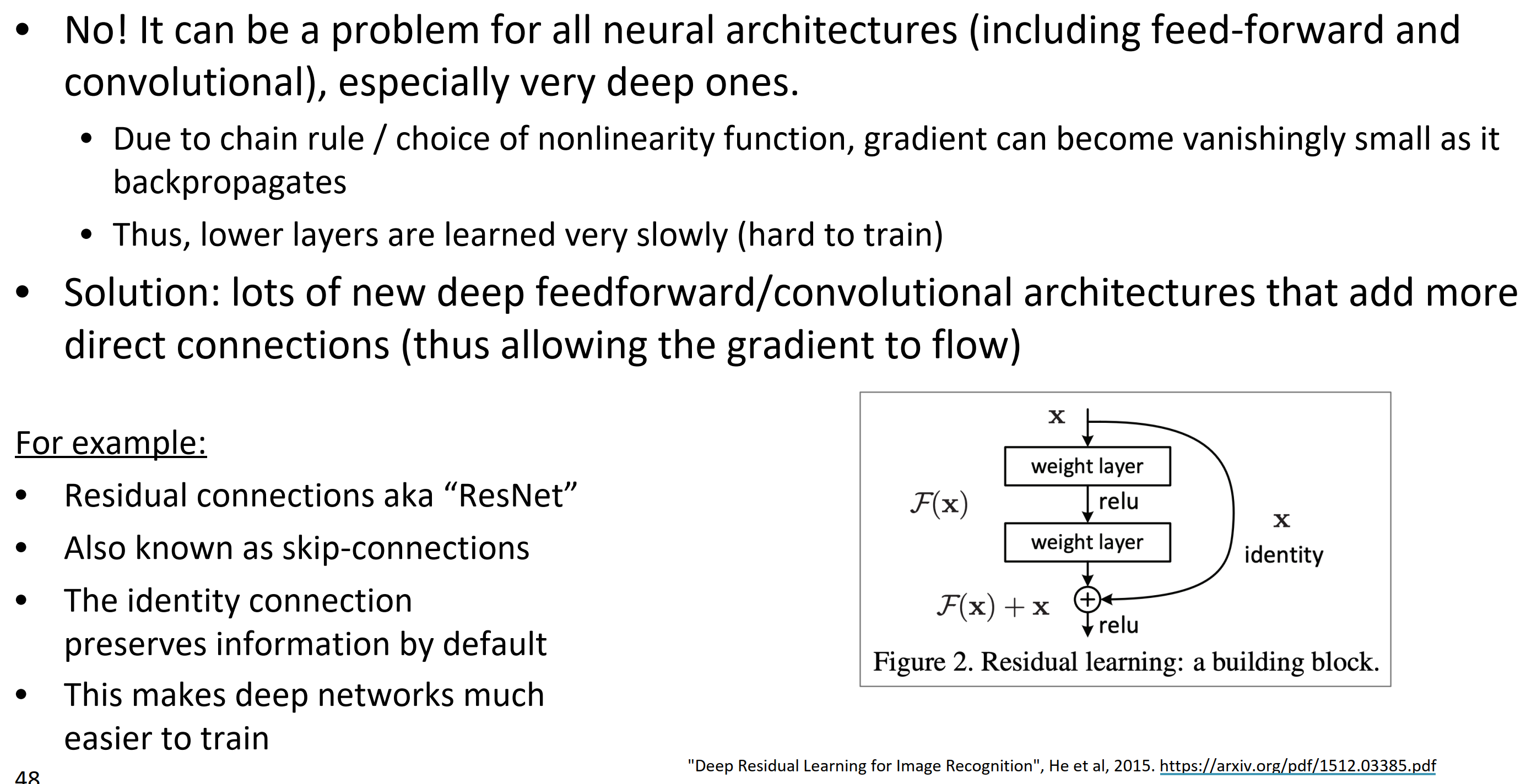
Solution: 许多新的深层前馈/卷积结构,添加更直接的连接(这允许梯度流向更远)
例子:
- 残差连接,“Resnet”
- 跳跃连接
- 通过默认保留信息的相同连接
- 这些深度网络更容易训练
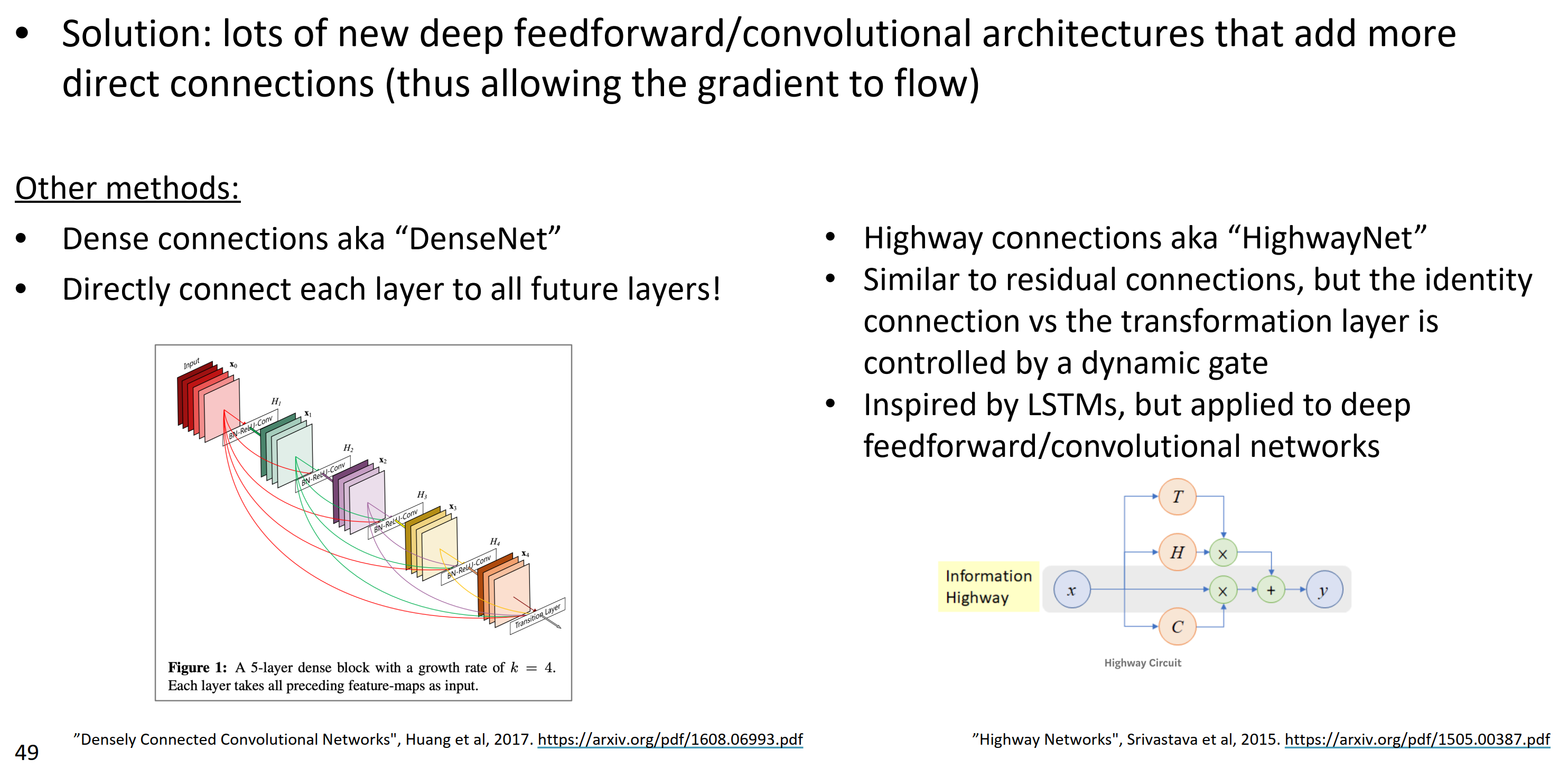
其它方法:
- 稠密连接的, “DenseNet”
- 直接连接所有将来的层
- 高速公路连接, “HighwayNet”
- 类似于残差连接,但是等同连接和变换层被一个动态门控制
- 受LSTMs的影响, 应用在深层前馈/卷积网络

总结:梯度消失和梯度爆炸是普遍问题,RNNs尤其不稳定,是因为重复使用相同权重矩阵。
Bidirectional and Multi-layer RNNs: motivation
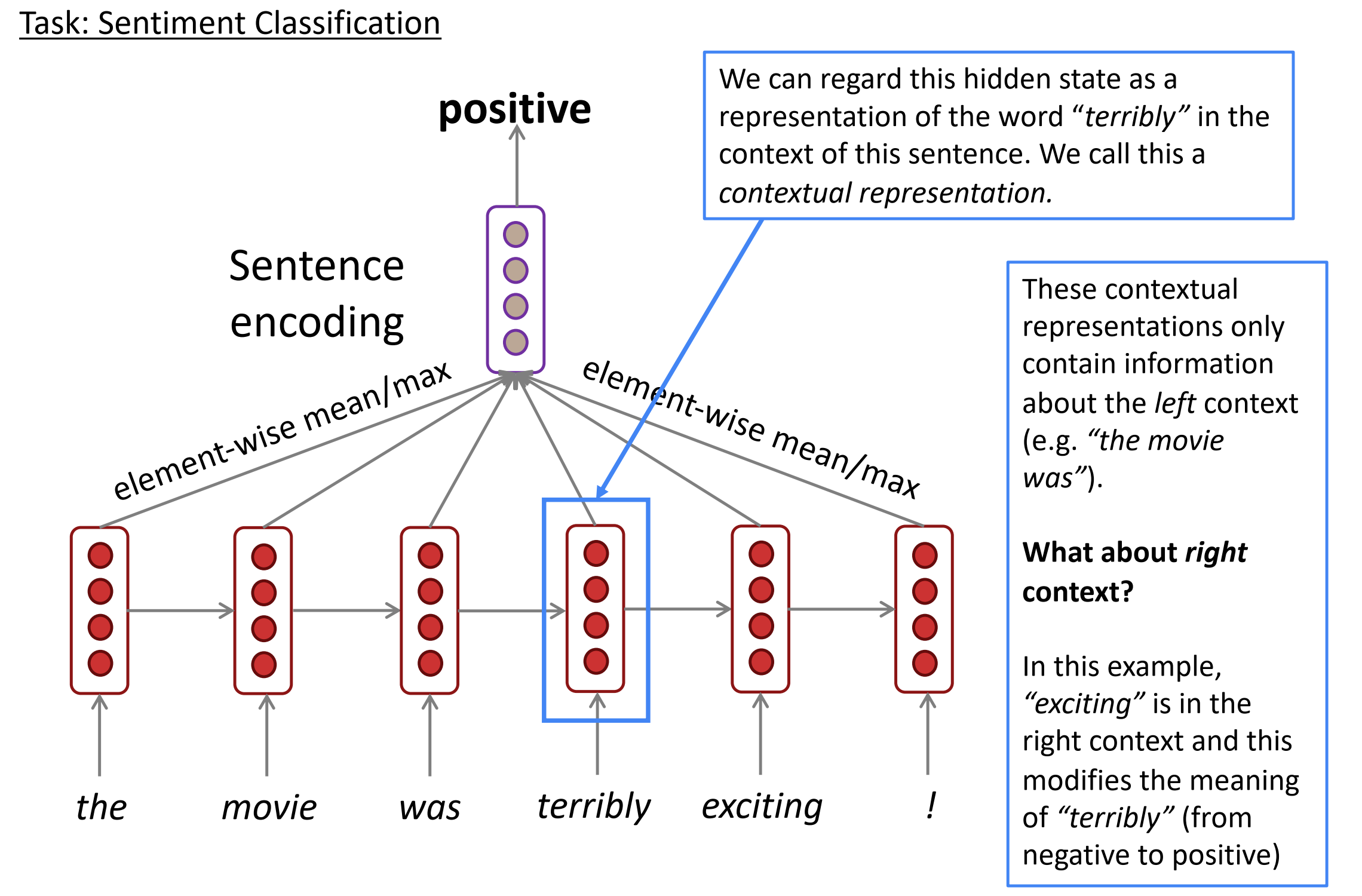
在情感分类任务中,
- 我们可以把隐藏状态看作是这个句子中单词terribly的上下文表示。这个称之为上下文表示
- 这些上下文表示只包含左边上下文信息
- 那怎么表示右边上下文信息呢?
- 这个例子中,exciting是在右边的上下文,它修饰terribly的意思(从否定变为肯定)
Bidirectional RNNs
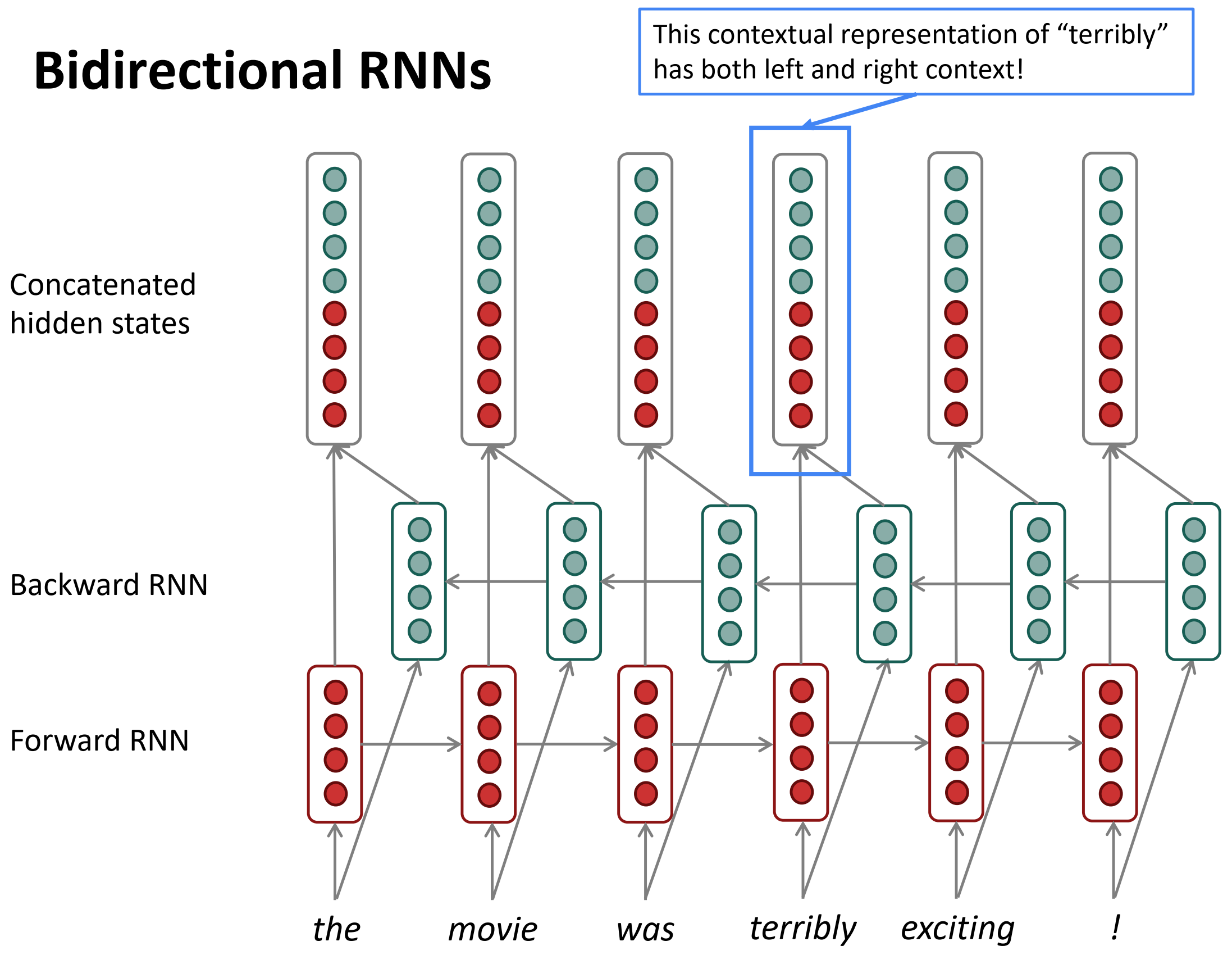
双向RNNs
上图中,结合后的隐层状态,绿色就可以表示右边的上下文。

双向RNNs,计算符号。
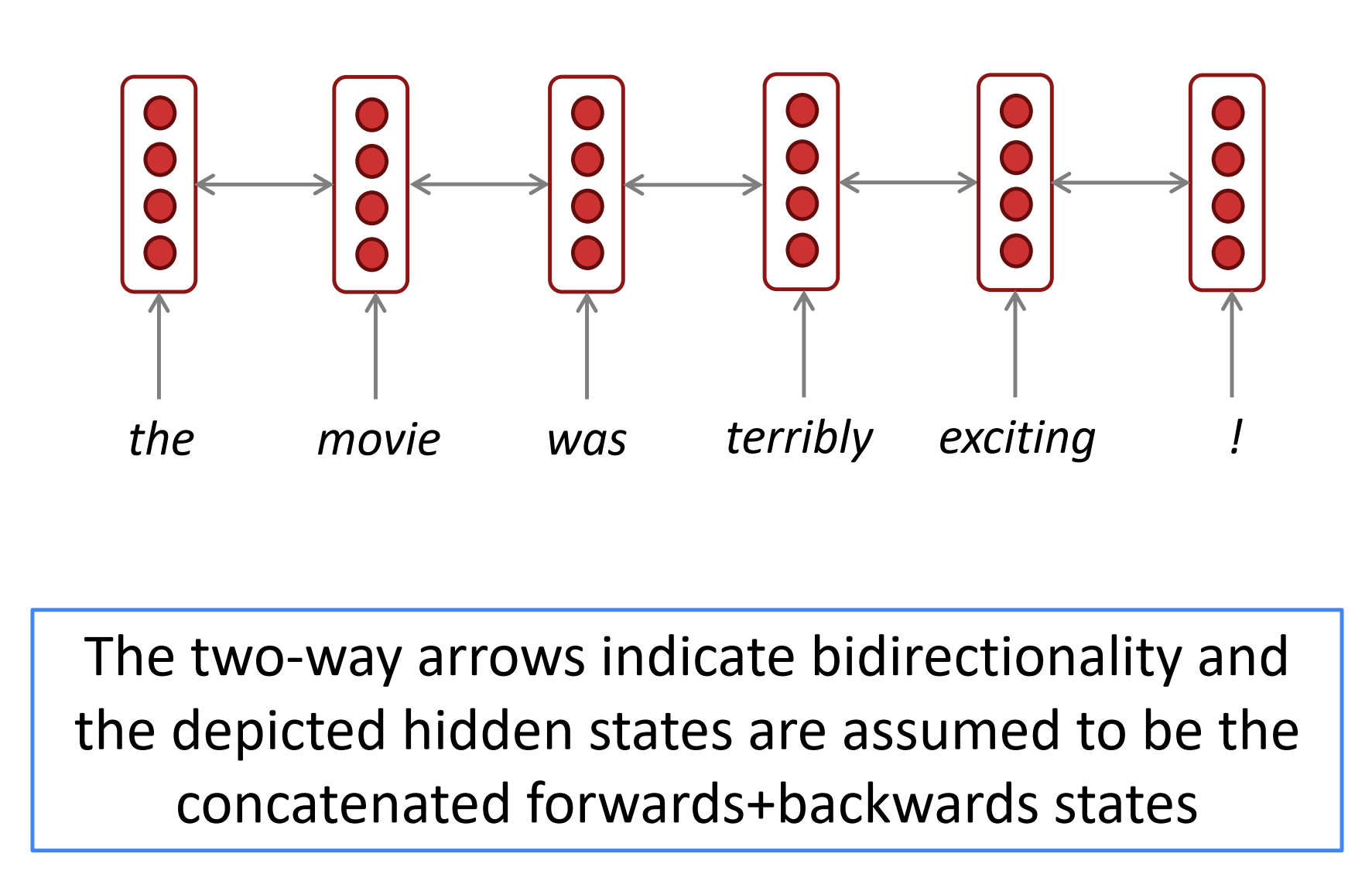
简化的双向RNN,双向箭头表示双向,和描述的隐层状态被假定为结合的前向和反向状态。

- 注意:双向RNNs只适用于,当你输入整个序列
- 它不适用于语言建模,因为LM你只有左边上下文。
- 如果你有整个上下文(比如,任何编码),双向是强大的(你要默认使用它)
- 例如,BERT(Bidirectional Encoder Representations from Transformers )是基于双向的强大预训练上下文表示系统。
- 你将在几周后学习更多包含BERT的transformers
Multi-layer RNNs

- RNNs在一个维度上已经很深了(展开到许多时刻)
- 我们通过应用多层RNNs来让其在另一个维度deep
- 这允许神经网络计算更复杂的表达
- 低层RNNs应该计算低层特征,而高层RNNs应该计算高层
- 多层RNNs也叫作堆叠RNNs
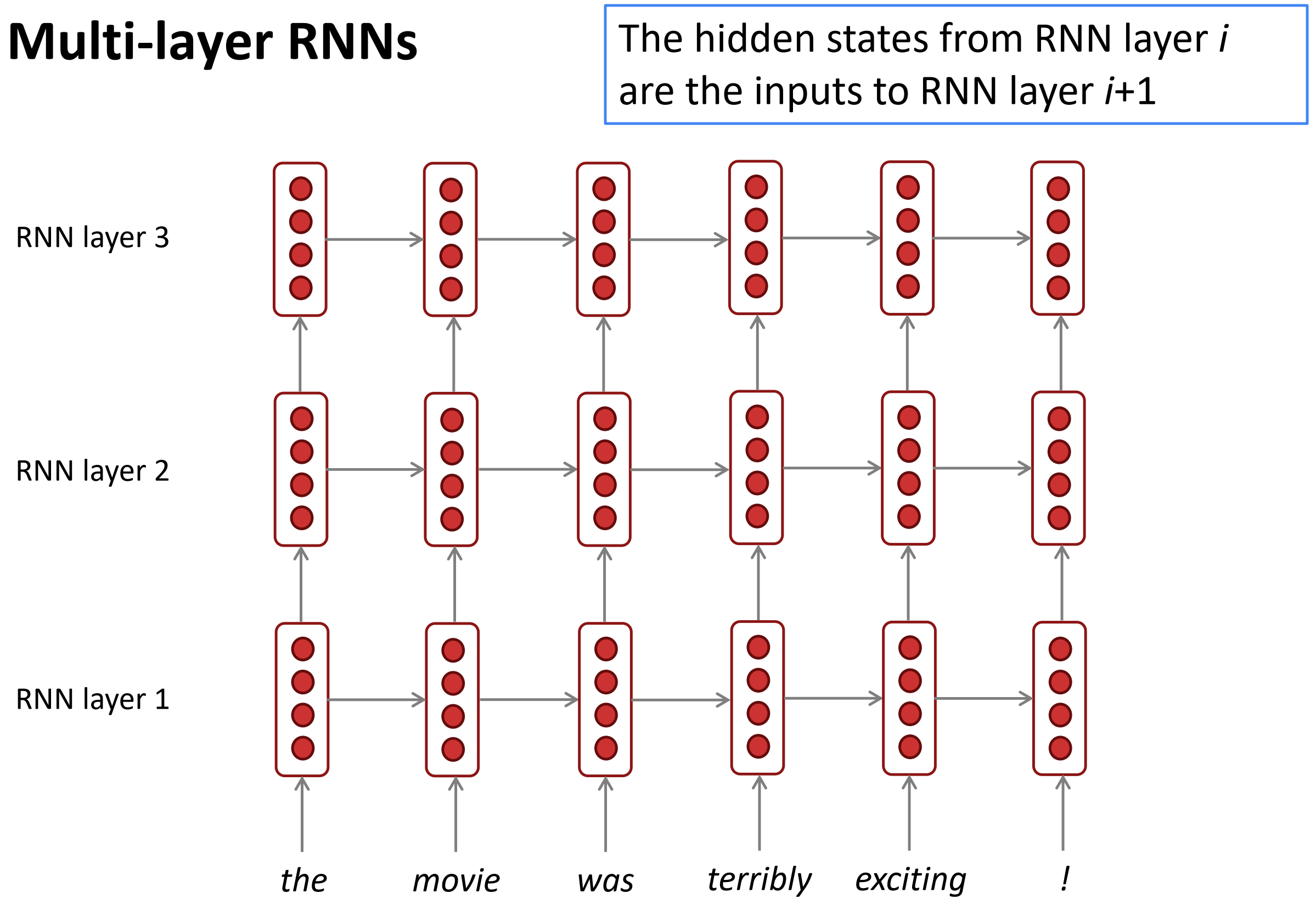
RNNs的第i层隐层状态就是第i+1层的输入。
Multi-layer RNNs in practice

- 高表现的RNNs经常是多层的(但没有卷积或前馈网络那么深)
- 例如,在2017年一篇论文,Britz et al发现神经机器翻译,2 to 4 层RNN编码器是最好的, 4层解码器是最好的。
- 通常, 跳跃连接/稠密连接是在训练深度RNNs需要的
- 基于Transformer的神经网络(如,BERT)通常是深层的,像12层或24层
- 其有很多skipping-like连接
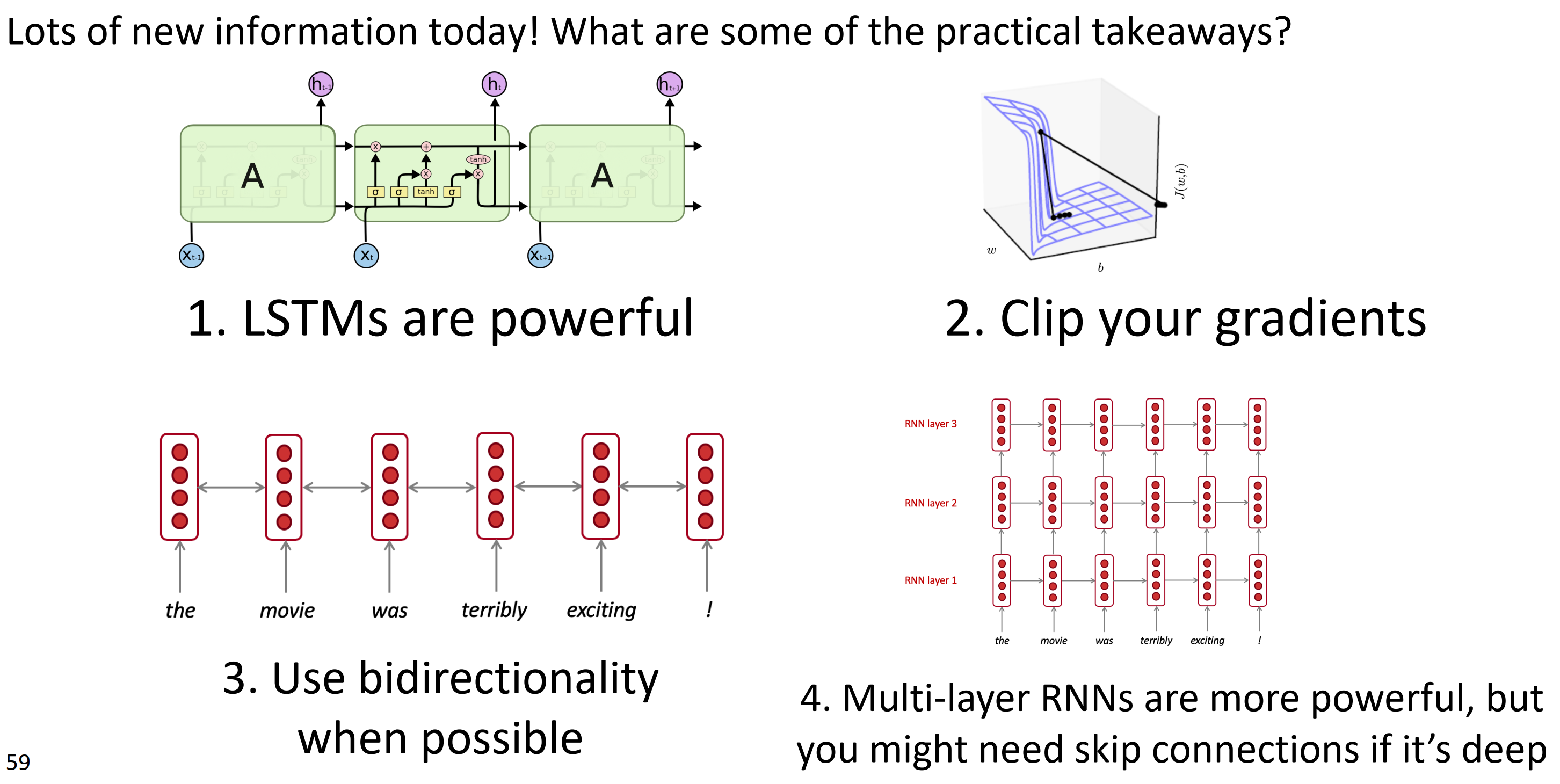
总结
参考
[1] cs224n-2019-notes05-LM_RNN
[2] cs224n-2021-lecture06-fancy-rnn
[3] Recurrent Neural Networks Tutorial, Part 3
[5] CS224N(1.24)Language Models and RNNs
[6] Science is interesting.07 Vanishing Gradients and Fancy RNNs
[7] 2019年CS224N课程笔记-Lecture 7: Vanishing Gradients and Fancy RNNs






