6. Capsule net 论文笔记

6. Capsule net 论文笔记

本文是2017年深度学习奠基人Geoffrey Hintons的 Dynamic Routing Between Capsules笔记。

摘要

一个capsule胶囊是一组神经元，其激活向量(就是低层的输入向量)表示的是特定类型的实体(如对象或对象的部分)的实例化参数。本文使用激活向量的长度来表示实体存在的概率和其方向来表示实例化后的参数。活的胶囊通过变换矩阵在低一层做预测，然后作为高层胶囊的实例化参数。当多个预测一致时，高层胶囊激活。本文在求低层到高层胶囊的权重时没有使用反向传播，而使用动态路由来更新：低层胶囊偏好将其输出传送到高层胶囊，使其激活向量和预测值的点积值较大。

胶囊网络计算过程

上图来源于 Understanding Hinton’s Capsule Networks. Part 2. How Capsules Work..

Step1: 预测向量$\hat{\mathbf{u}}_{j|i}$。

如上图左侧$\mathbf{u}_{i} \in \mathbb{R}^{k \times 1}, i=1,2, \ldots, n$表示低层胶囊输入，$n$表示胶囊数目。图示就是3个，$k$表示每个胶囊激活向量的长度。比如$\mathbf{u}_1$表示眼睛这种低层胶囊特征，(其它向量分别表示鼻子、嘴巴等特征用来检测人脸)，作者会将其转换成所谓的预测向量$\hat{\mathbf{u}}_{j|i}$，就是乘以一个转换矩阵:

$$\hat{\mathbf{u}}_{j \mid i}=\mathbf{W}_{i j} \mathbf{u}_{i} \tag{1}$$

这个矩阵$\mathbf{W}_{i j}$是通过反向传播学习的。

Step2: 高层胶囊$j$输入$\mathbf{s}_{j}$。

然后将得到的预测向量$\hat{\mathbf{u}}_{j \mid i}$进行加权求和:

$$\mathbf{s}_{j}=\sum_{i} c_{i j} \hat{\mathbf{u}}_{j \mid i} \tag{2}$$

这就是图示“求和“符号部分的数学表示，其中$c_{i j}$是权重系数，论文中叫耦合系数(coupling coefficients),由动态路由算法决定。并且要满足$\sum_j c_{i j}=1$。其表示低层胶囊$i$对高层胶囊$j$的权重大小。这样，作者就得到了高层胶囊$j$的输入$\mathbf{s}_{j}$。

coupling coefficients that are determined by the iterative dynamic routing process

Step 3: 高层胶囊$j$输出$\mathbf{v}_{j}$。

如图示Squash函数部分，即将得到的输入经过squash函数获得输出$\mathbf{v}_{j}$。因为胶囊网络是拿胶囊的向量的模长来表示高层胶囊表示的实体存在的概率。因此，论文提出了非线性函数squashing。其可以保证短向量压缩趋于0，长向量趋近于1，并且保持向量方向不变。

use a non-linear “squashing” function to ensure that short vectors get shrunk to almost zero length and long vectors get shrunk to a
length slightly below 1.

$$\mathbf{v}_{j}=\frac{\left\|\mathbf{s}_{j}\right\|^{2}}{1+\left\|\mathbf{s}_{j}\right\|^{2}} \frac{\mathbf{s}_{j}}{\left\|\mathbf{s}_{j}\right\|} \tag{3}$$

• 当$\mathbf{s}_{j}$是一个长向量，那么$\mathbf{v}_{j}\rightarrow \frac{\mathbf{s}_{j}}{\left\|\mathbf{s}_{j}\right\|}$
• 当$\mathbf{s}_{j}$是一个短向量，那么$\mathbf{v}_{j}\rightarrow \left\|\mathbf{s}_{j}\right\|\mathbf{s}_{j}$

squash函数1D可视化图如下:(可以看看其趋近值)

import torch
import torch.nn.functional as F

T_EPSILON = 1e-6
def squash(x, axis=-1):
    """
    不是公式3原始的样子, 简化成趋近长向量计算
    text version of squash, slight different from original one
    :param x: vector
    :param axis: int
    :return: vector
    """
    s_squared_norm = (x ** 2).sum(axis, keepdim=True)
    scale = nn.sqrt(s_squared_norm + T_EPSILON)
    return x / scale

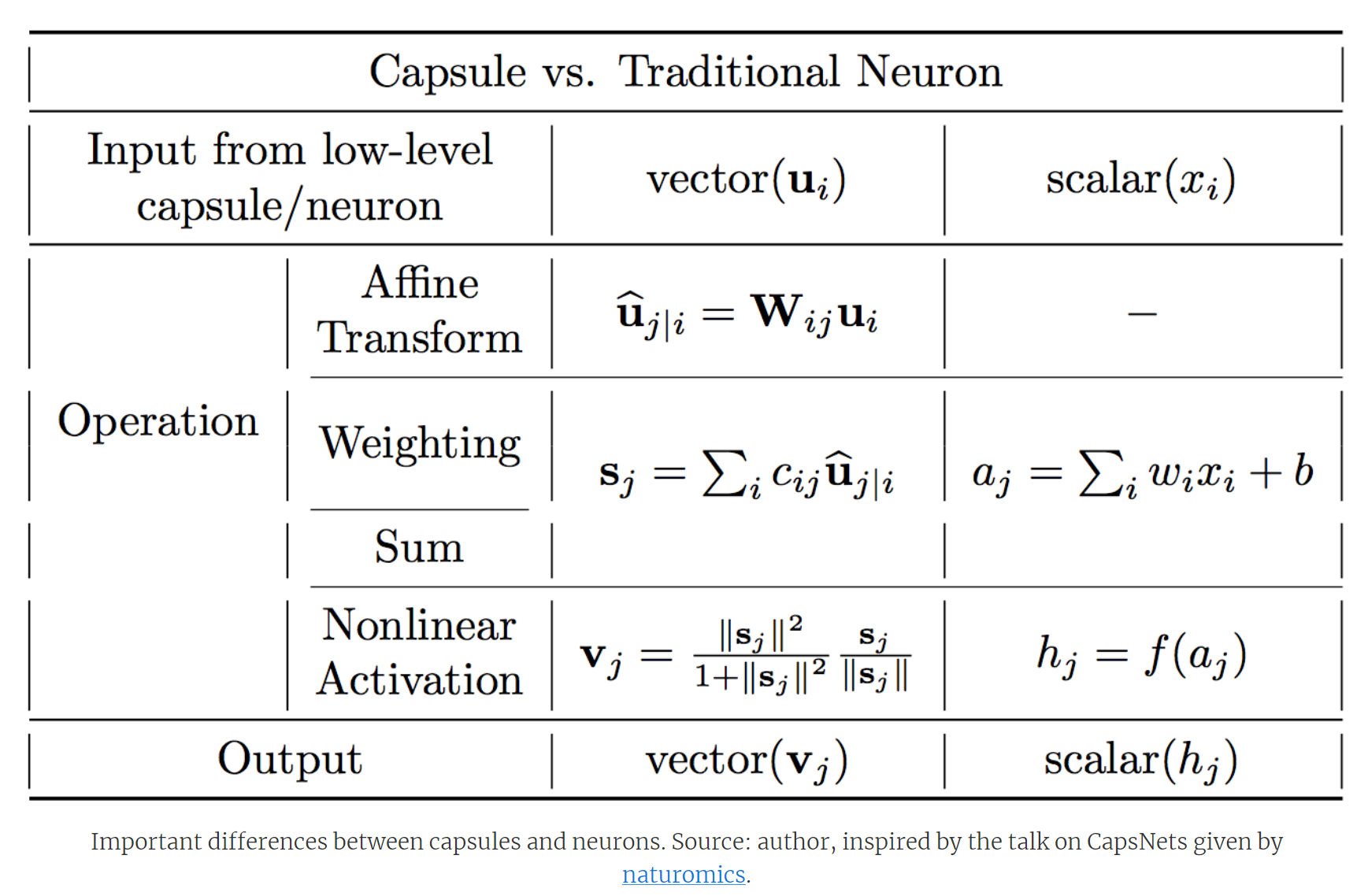
贴个胶囊网络和普通神经网络的区别表:(也来自于[1])。

注：胶囊网络胶囊输入是向量，神经网络神经元输入是标量。

现在经过3个步骤梳理作者大概知道高层胶囊$j$输出$\mathbf{v}_{j}$是怎么计算的。转换矩阵$\mathbf{W}_{i j}$可以用反向传播算法学习得到，但第二步中

耦合系数$c_{i j}$是通过所谓的动态路由算法来更新的，那么到底是怎么计算的呢？

动态路由算法

动态路由算法伪代码:

按照行号逐一解释:

1. 定义算法输入:低层$l$,(因为胶囊网络也是多层的，它的高层输入来自于低层的输出)；该低层$l$所有胶囊的输出$\hat{\mathbf{u}}_{j \mid i}$,（就是低层胶囊$i$经过转换矩阵变换成的向量输入到高层胶囊$j$; 以及路由迭代次数(超参数，一般设置为3,或4).
2. 定义一个临时变量$b_{ij}$,初始化为0.用于迭代计算低层胶囊$l$中胶囊$i$到高层$l+1$中胶囊$j$.
3. 迭代$r$次.
4. 将$b_{ij}$经过softmax转换为总和为1的类概率权重，其实，第一轮$c_{ij}=1/\max(j)$都相等.高层胶囊数目$\max(j)$, (按照最大熵也应该是这样).
5. 按照上面式2，作者就可以求出高层胶囊输入$\mathbf{s}_{j}$.
6. 类似地按照式3求出高层胶囊$j$输出$\mathbf{v}_{j}$.
7. 将$b_{ij}$更新为$b_{ij}+\hat{\mathbf{u}}_{j \mid i} \cdot \mathbf{v}_{j}$.因为$\hat{\mathbf{u}}_{j \mid i} \cdot \mathbf{v}_{j}$如果是正值且越来越大的话表示$\hat{\mathbf{u}}_{j \mid i}$与$\mathbf{v}_{j}$越来越相似。(这个过程也有点类似于聚类,如李宏毅教授Capsule)

最后返回高层胶囊$j$输出$\mathbf{v}_{j}$.给个简化示例:

def dynamic_routing(x, num_caps, dim_caps, routings=4):
    batch_size = x.size(0)
    input_num_capsule = x.size(1)
    W = torch.randn(batch_size, input_num_capsule, num_caps*dim_caps)
    u_hat_vecs = torch.matmul(x, W)
    u_hat_vecs = u_hat_vecs.view((batch_size, input_num_capsule, num_caps, dim_caps))

    #交换维度变成:batch_size, num_caps, input_num_capsule, dim_caps
    u_hat_vecs = u_hat_vecs.permute(0, 2, 1, 3)
    #初始化一个[batch_size, num_caps, input_num_capsule]全0的矩阵b, 4, 2, 3
    b = torch.zeros_like(u_hat_vecs[:, :, :, 0])

    for i in range(routings):
        b = b.permute(0, 2, 1)
        c = F.softmax(b, dim=2)
        c = c.permute(0, 2, 1)#换回原来维度
        b = b.permute(0, 2, 1)
        #c * u hat vector 过squash得到输出v eisnum 在k这个维度求和
        #其代表dim_caps即每个胶囊维度上求和
        v = squash(torch.einsum('bij, bijk->bij', (c, u_hat_vecs)))
        if i < routings -1: #如果不到迭代次数 继续求和
            b = torch.einsum('bij, bijk->bij', (v, u_hat_vecs))
    return v

x = torch.randn((4, 3, 3))
print(x)
num_caps = 2
caps_dim = 3
v_out = dynamic_routing(x, num_caps, caps_dim, routings=3)
print(v_out, v_out.shape)

Inference

[1] Understanding Hinton’s Capsule Networks

[2] Dynamic-Routing-Between-Capsules

[3] 浅谈胶囊网络与动态路由算法

[4] capsule-network