np.convolve 使用

4. np.convolve 使用

1. np.convolve 基本定义

numpy 中实现卷积操作的函数 numpy 官方文档，定义为:
convolve(a, v, mode='full'),其中，
a和v都是1-d的array, 长度为N,M。 注意一点:

If v is longer than a, the arrays are swapped before computation.
一旦v比a长，就要交换两个数组，就是a与v对应公式中的位置互换。这是因为，按照如下官方计算公式，不然会出现$v[n-m]$的index是个负数。

$(a * v)[n]=\sum_{m=-\infty}^{\infty} a[m] v[n-m]$，

mode可选3种方式:

• full: 默认值，返回每一个卷积值，长度是N+M-1,在卷积的边缘处，信号不重叠，存在边际效应。
• same: 返回值长度与$\max(M, N)$，还是存在边际效应。
• valid: 返回值长度为$\max(M, N) - \min(M, N) + 1$，这时计算只在两个输入的重叠部分进行，没有边际效应。实际中一般用这个。

2. np.convolve 计算

Stackoverflow上有个问题，能很好说明np.convolve计算的详细过程。 how dose numpy.convolve do its job?
对于，np.convolve([3, 4], [1, 1, 5, 5], 'valid'), 输出为什么是 array([ 7, 19, 35])。
因为卷积就是两个函数在共同区间的求积的过程，卷积公式：

教科书上一般定义函数 $f, g$的卷积 $f * g(n)$ 如下,

• 连续形式:

$$(f * g)(n)=\int_{-\infty}^{\infty} f(\tau) g(n-\tau) d \tau$$

• 离散形式:

$$(f * g)(n)=\sum_{\tau=-\infty}^{\infty} f(\tau) g(n-\tau)$$

具体计算过程如下：

1.翻转[4, 3] 为 [3, 4]。

2.逐步平移并求积：

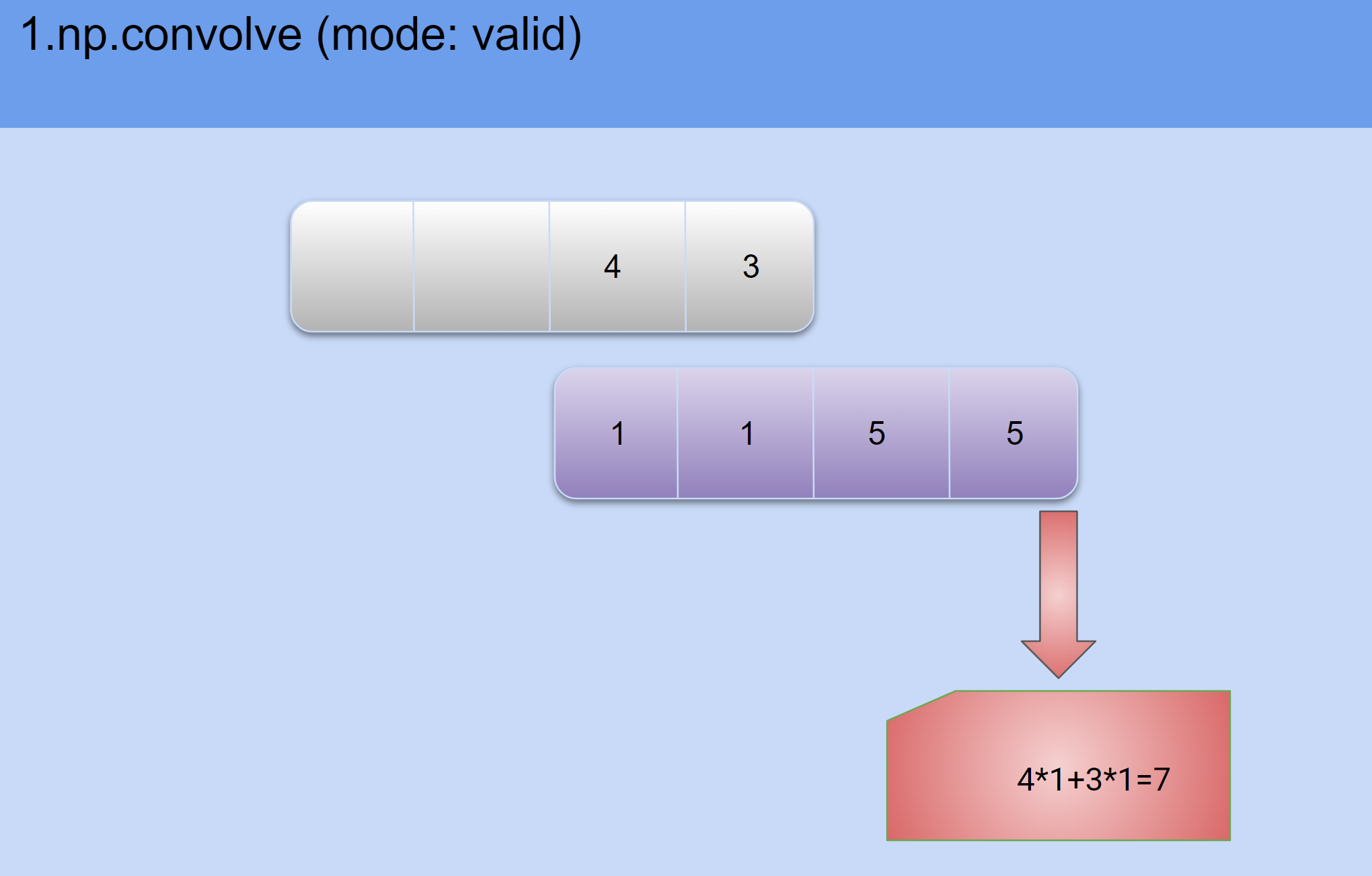
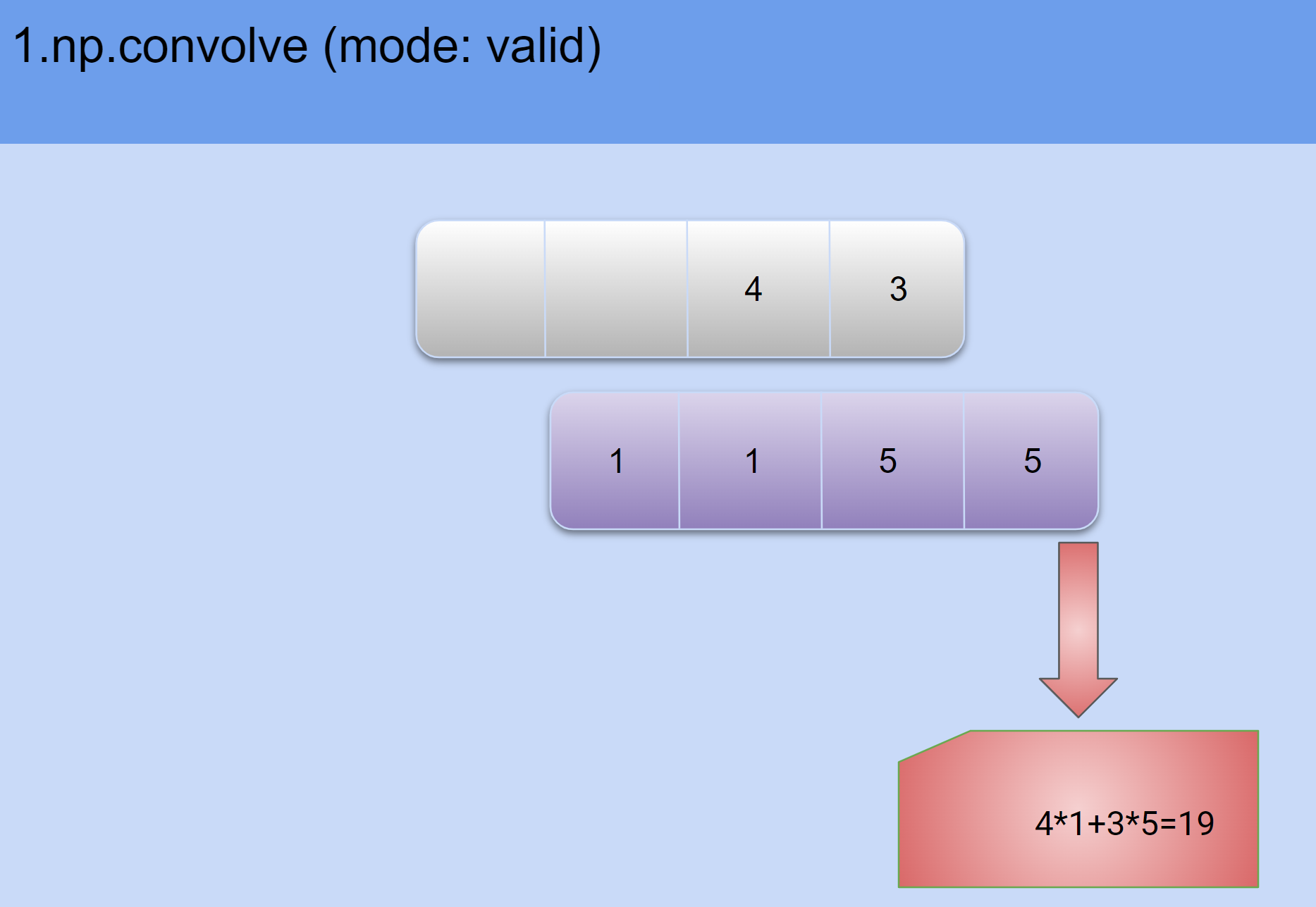
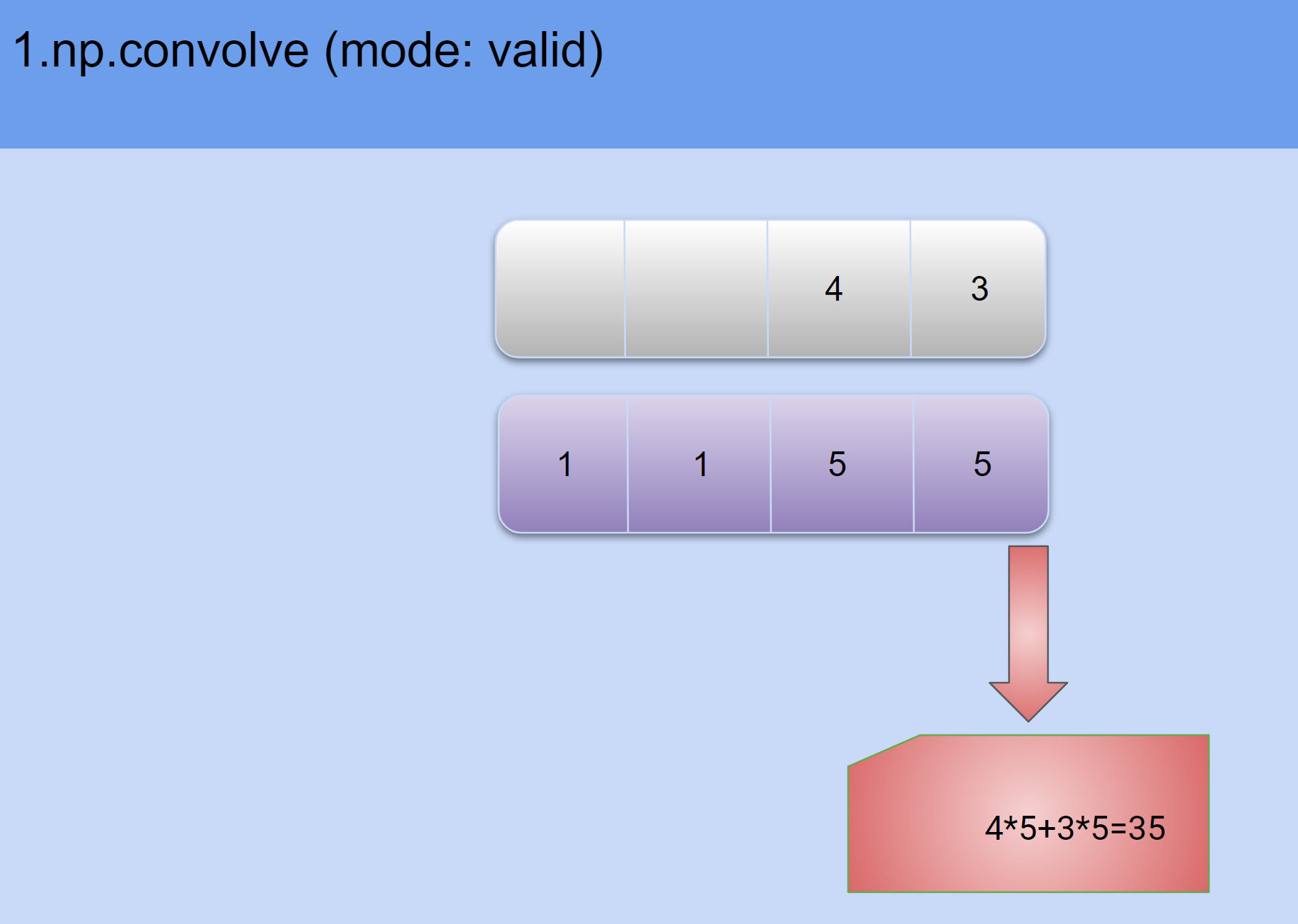
1. 得到最后结果，np.convolve([3, 4], [1, 1, 5, 5], 'valid')=array([ 7, 19, 35])

那么，np.convolve([3, 4], [1, 1, 5, 5], 'full')呢？同样翻转，然后两函数累积如下:

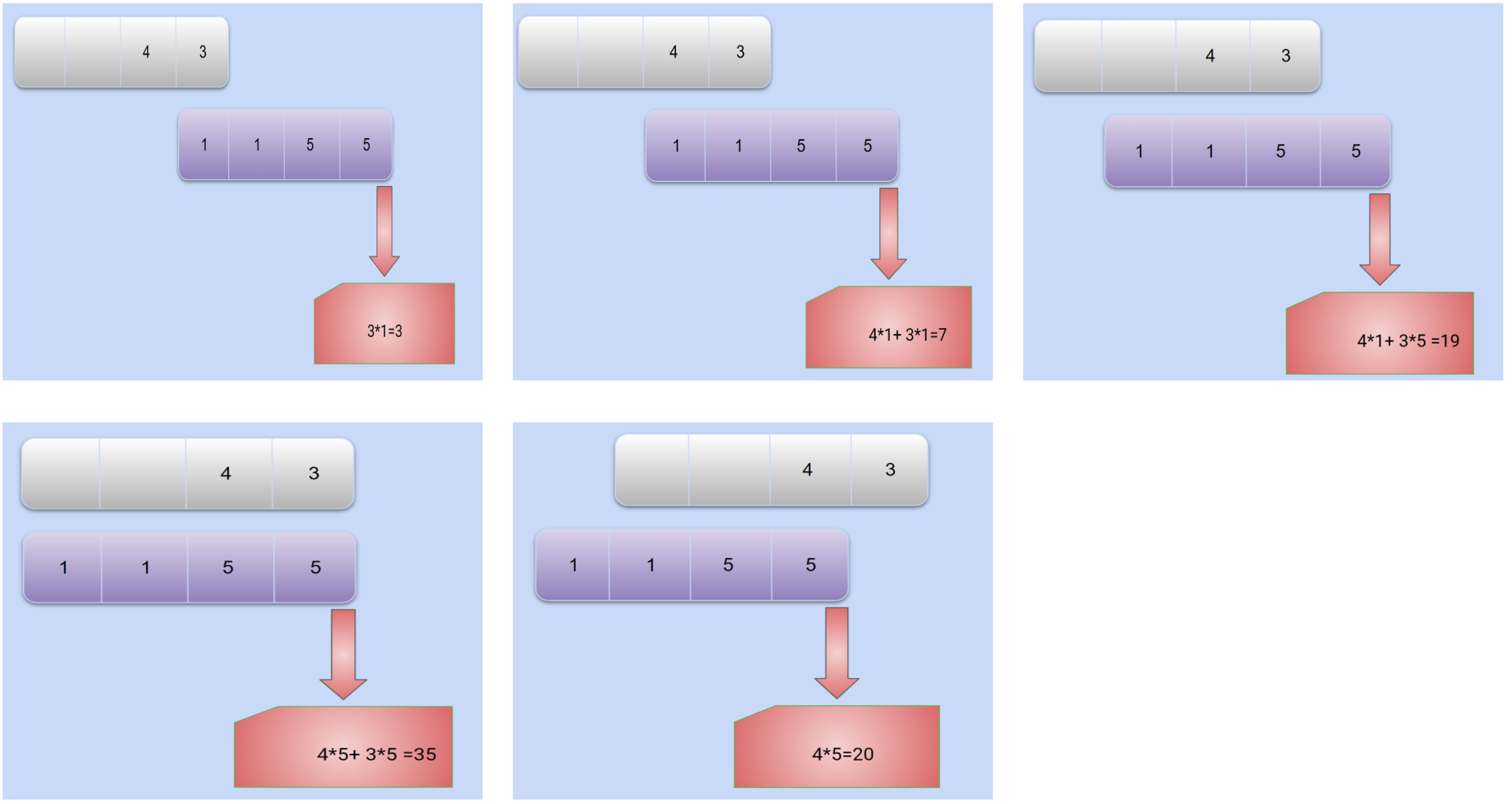
结果为：array([ 3, 7, 19, 35, 20]).

同样地可得到,

np.convolve([3, 4], [1, 1, 5, 5], 'same')=array([ 3, 7, 19, 35])

Inference

[1] 如何通俗易懂地解释卷积？

[2] python 卷积