机器学习-白板推导 10. EM 算法

1. EM算法导出

本文中所有的参数定义如下：

$\begin{align} &X: \text{ observed data }\\ &Z: \text{ unobserved data }\\ &(X, Z): \text{ complete data }\\ &\theta: \text{ parameter }\\ \end{align}$

EM是Expectation Maximization简写，意为期望最大, 用于含有隐变量的概率模型参数的极大似然估计。我们经常说的极大似然估计是对于概率分布 $P(X|\theta)$ ,求解使得其最大的算法：

$\theta_{MLE} = \text{argmax}_{\theta} \log P(X|\theta) \tag{1}$

对于式1如果引入隐变量 $Z$ ，要满足 $P(X) = \int_Z P(X|Z)P(Z)$ .如果是离散量就改成求和。那么可改写成：

$L(\theta) = \log P(X|\theta) = \log \int_Z P(X, Z|\theta) =\log \left(\int_Z P(X|Z, \theta)P(Z|\theta) \right) \tag{2}$

实际上式2是非常难计算，因为有未观测数据并含有积分的对数。

而对 $\log P(X|\theta)$ 利用条件概率有：

$\begin{align} \log P(X|\theta) &= \log \frac{P(X, Z|\theta)}{P(Z|X, \theta)}\\ &= \log P(X, Z|\theta)- \log P(Z|X, \theta)\\ &= \left ( \log P(X, Z|\theta) -\log Q(Z)\right )- \left(\log P(Z|X, \theta)-\log Q(Z)\right)\\ &= \log\frac{ P(X, Z|\theta)}{ Q(Z)} - \log \frac{P(Z|X, \theta)}{Q(Z)} \end{align} \tag{3}$

其中，引入的 $Q(Z) \neq 0$ 是关于 $Z$ 的分布。

现在对式3左右两边同时求关于 $Q(Z)$ 的期望：

$\begin{align} \text{左边} &= \int_Z Q(Z) \cdot \log P(X|\theta) dZ\\ &= \log P(X|\theta) \int_Z Q(Z) dZ\\ &=\log P(X|\theta) \end{align} \tag{4}$

右边变成：

$\begin{align} \text{右边} &=\color{red}{\underbrace{\int_Z Q(Z) \cdot \log\frac{ P(X, Z|\theta)}{ Q(Z)}dZ}_{ELBO}} \color{green}{\underbrace{-\int_Z Q(Z) \cdot \log \frac{ P(Z|X, \theta)}{ Q(Z)}dZ}_{KL}}\\ \end{align} \tag{5}$

其中，前半部分是ELBO，evidence lower bound。后半部分是 $KL(Q(Z)||P(Z|X, \theta))$ 。

KL散度是用来衡量两个分布相似度(距离)：
$\begin{aligned} \text{KL} (p||q) &= E_q[ -\text{log}\frac{p(x)}{q(x)}] \ge -\text{log} E_q[\frac{p(x)}{q(x)}] \\&=-\text{log} [\int q(x) \frac{p(x)}{q(x)}dx] \\&= -\text{log}\int_{x} p(x)dx = -\text{log} 1= 0 \end{aligned}$

因此， $KL(Q(Z)||P(Z|X, \theta)) \ge 0, \quad 当且仅当 Q(Z) = P(Z|X, \theta)时取等号$ 。根据式3， 4， 5可知，当KL部分取等号时， $\log P(X|\theta) = \text{ELBO}$ ，也就是说ELBO是其下界。

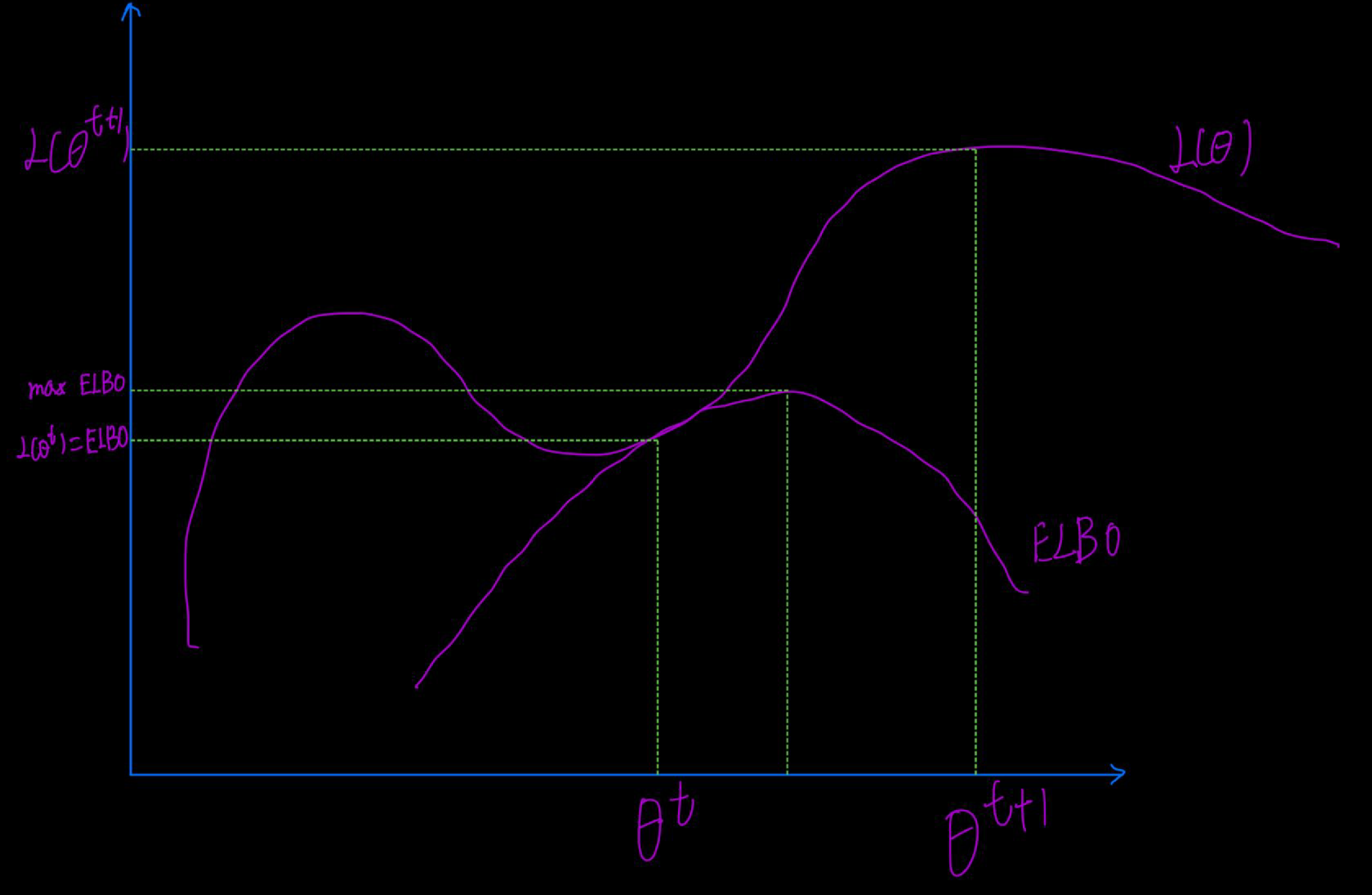
如上图所示， $L(\theta)$ 和ELBO都是关于 $\theta$ 的函数，且从定义上看， $L(\theta) \ge \text{ELBO}$ ,也就是 $L(\theta)$ 图像总在ELBO上面。我们用迭代法来寻找最优解，当前仅当 $Q(Z) = P(Z|X, \theta^t)$ 时，能使得 $L(\theta) = \text{ELBO}$ ，并且因为迭代法要求 $\theta^{t+1}$ 使得 $L(\theta^{t+1}) \ge L(\theta^{t})$ 。实际上，先赋予初值 $\theta^0$ ,求出ELBO的期望，然后求下一个 $\theta^1$ ,直到ELBO值大于 $\theta^0$ 对应的，用 $\theta^1$ 替换掉 $\theta^0$ ，直到找到 $ELBO$ 最大的参数，这时也是 $L(\theta)$ 最大的参数。其公式就是：

$\begin{align} \theta^{t+1} &= \text{argmax}_\theta \text{ ELBO}\\ &= \text{argmax}_\theta \int_Z Q(Z) \cdot \log \frac{P(X, Z|\theta)}{ Q(Z)}dZ\\ &= \text{argmax}_\theta \int_Z P(Z|X, \theta^t) \cdot \log \frac{ P(X, Z|\theta)}{ P(Z|X, \theta^t)}dZ\\ &=\text{argmax}_\theta \int_Z P(Z|X, \theta^t) \cdot \log P(X, Z|\theta) dZ -\underbrace{\text{argmax}_\theta \int_Z P(Z|X, \theta^t) \cdot \log P(Z|X, \theta^t)}_{与\theta无关} dZ\\ &= \text{argmax}_\theta \int_Z P(Z|X, \theta^t) \cdot \log P(X, Z|\theta) dZ\\ &= \text{argmax}_\theta E_{P(Z|X, \theta^t)}[\log P(X, Z|\theta)] \end{align} \tag{6}$

总结：EM算法适用于含有隐变量的极大似然估计，由于含隐变量的的积分和对数难于计算，转化为求ELBO的最大值，EM算法公式如下：

$\begin{align} \theta^{t+1} &=\text{argmax}_\theta \int_Z \log P(X, Z|\theta) P(Z|X, \theta^t) dZ\\ &= \text{argmax}_\theta E_{P(Z|X, \theta^t)}[\log P(X, Z|\theta)] \end{align} \tag{7}$

最重要的两步：

E step：计算 $\log P(X,Z|\theta)$ 在概率分布 $P(Z|X, \theta^t)$ 下的期望。
M step: 计算使得这个期望最大化的参数 $\theta$ 。

2. EM 公式导出另外一种方法 (Jensen 不等式)

对公式2引入隐变量分布 $Q(Z)$ :

$\begin{align} \log P(X|\theta) &= \log\int_Z P(X, Z|\theta)dZ\\ &= \log\int_Z \frac{P(X, Z|\theta)}{Q(Z)}Q(Z)dZ\\ &= \log E_{Q(Z)} [\frac{P(X, Z|\theta)}{Q(Z)}]\\ &\ge \underbrace{E_{Q(Z)} [\log\frac{P(X, Z|\theta)}{Q(Z)}]}_{ELBO}\\ \end{align} \tag{8}$

其中，最后一步是利用Jensen不等式，对于凹函数 $f(x), 有 f(E[x]) \ge E[f(x)])$ 。其实最后结果就是ELBO。当且仅当 $\frac{P(X, Z|\theta)}{Q(Z)}= C(常数)$ 时，可取等号。

$\begin{align} &\frac{P(X, Z|\theta)}{Q(Z)} = C \\ &\Longrightarrow Q(Z) = \frac{1}{C} P(X,Z|\theta)\\ &\Longrightarrow \int_ZQ(Z) dZ= \int_Z\frac{1}{C} P(X,Z|\theta)dZ\\ &\Longrightarrow 1 = \frac{1}{C}P(X|\theta)\\ &\Longrightarrow P(X|\theta) = C\\ &\Longrightarrow Q(Z) = \frac{P(X, Z|\theta)}{P(X|\theta)}=P(Z|X, \theta) \end{align} \tag{9}$

这表明引入 $Q(Z)$ 要等于后验分布 $P(Z|X, \theta)$ 。而这时，优化目标 $\log P(X|\theta = \text{ELBO}$ ，其它迭代优化过程跟第一小节一样。

3. EM算法的收敛性

使用迭代算法来求 $L(\theta)$ 的最大值，即我们希望新的估计值 $\theta$ 能使得 $L(\theta)$ 变大，就是 $L(\theta^{t+1}) \ge L(\theta^t)$ ,其中 $L(\theta^t)$ 是t次迭代后的值，这跟第一小节推导非常类似。

而要证明 $P(X|\theta^{t+1}) \ge P(X|\theta^{t})$ ，我们先用条件概率公式转换下：

$L(\theta) = \log P(X|\theta) = \log \frac{P(X, Z|\theta)}{P(Z|X, \theta)} = \log P(X, Z|\theta)- \log P(Z|X, \theta) \tag{10}$

我们对式10两边同时求关于 $P(Z|X, \theta^t)$ 的期望：

$\begin{align} \text{左边} &= \int_Z P(Z|X, \theta^t) \cdot \log P(X|\theta) dZ\\ &= \log P(X|\theta) \int_Z P(Z|X, \theta^t) dZ\\ &=\log P(X|\theta) \end{align} \tag{11}$

其中， $\int_Z P(Z|X, \theta^t) dZ = 1$ 。而右边有:

$\begin{align} \text{右边} &= \int_Z P(Z|X, \theta^t) \cdot\log P(X, Z|\theta)dZ- \int_Z P(Z|X, \theta^t) \cdot \log P(Z|X, \theta) dZ\\ \end{align} \tag{12}$

我们将前半部分记为 $Q(\theta, \theta^t) = \int_Z P(Z|X, \theta^t) \cdot\log P(X, Z|\theta)dZ$ 在EM算法中称为Q function, 其实就是上面ELBO，也就是EM算法迭代目标式。

后半部分记为 $H(\theta, \theta^t) = \int_Z P(Z|X, \theta^t) \cdot \log P(Z|X, \theta) dZ$ 。那么根据式10、11和式12有：

$\begin{align} \log P(X|\theta) &= \int_Z P(Z|X, \theta^t) \cdot\log P(X, Z|\theta)dZ- \int_Z P(Z|X, \theta^t) \cdot \log P(Z|X, \theta) dZ\\ &=Q(\theta, \theta^t) - H(\theta, \theta^t) \end{align} \tag{13}$

对于 $Q(\theta, \theta^t)$ ，由小节1可知 $Q(\theta^{t+1}, \theta^{t}) \ge Q(\theta^t, \theta^{t})$ ，那么 $H(\theta, \theta^t)$ 会怎么变化？

$\begin{align} &H(\theta^{t+1}, \theta^{t}) - H(\theta^t, \theta^{t}) \\ &= \int_Z P(Z|X, \theta^{t}) \cdot \log P(Z|X, \theta^{t+1}) dZ- \int_Z P(Z|X, \theta^t) \cdot \log P(Z|X, \theta^{t}) dZ\\ &= \int_Z P(Z|X, \theta^t) \log\frac{ P(Z|X, \theta^{t+1})}{ P(Z|X, \theta^{t})} dZ \\ &\le \log \int_Z P(Z|X, \theta^t)\frac{ P(Z|X, \theta^{t+1})}{ P(Z|X, \theta^{t})} dZ\\ &= \log \int_Z P(Z|X, \theta^{t+1}) dZ\\ &= \log 1=0 \end{align} \tag{14}$

其中，不等号变换使用Jensen不等式，如下式：

$\log \sum_{j} \lambda_{j} y_{j} \geq \sum_{j} \lambda_{j} \log y_{j}, \text { 其中 } \lambda_{j} \geq 0, \quad \sum_{j} \lambda_{j}=1 \tag{15}$

如果用KL散度易知，

$\int_Z P(Z|X, \theta^t) \log\frac{ P(Z|X, \theta^{t+1})}{ P(Z|X, \theta^{t})} dZ\\ = -\text{KL}(P(Z|X, \theta^t)||P(Z|X, \theta^{t+1})) \le 0 \tag{16}$

那么根据式14可知， $H(\theta^{t+1}, \theta^{t}) \le H(\theta^t, \theta^{t})$ ，也就是说 $H(\theta, \theta^t)$ 是递减的。综上根据式13可知， $L(\theta) = \log P(X|\theta)$ 是递增的，即 $\log P(X|\theta^t) \le \log P(X|\theta^{t+1})$ ,因此EM算法是收敛。

4. 广义EM算法

还是回到最开始的问题：最大化似然函数如式1所示。EM算法是为了解决参数估计中的问题，也就是learning问题：

$\hat \theta = \text{argmax}_\theta P(X|\theta) \tag{17}$

实际过程中，由于难于计算，我们利用条件概率公式将其转化为式3所示。从第一小节，式3， 4， 5可得：

$L(\theta) = \log P(X|\theta)=\text{ELBO} + KL(Q||P) \tag{18}$

这里我们定义ELBO为：

$L(Q, \theta) = \text{ELBO} = \int_Z Q(Z) \cdot \log\frac{ P(X, Z|\theta)}{ Q(Z)}dZ = E_{Q(Z)}[\log\frac{ P(X, Z|\theta)}{ Q(Z)}] \tag{19}$

另外，再写出KL散度部分：

$KL(Q||P) = \int_Z Q(Z) \cdot \log \frac{ Q(Z)}{ P(Z|X, \theta)}dZ = E_{Q(Z)}[ \log \frac{ Q(Z)}{ P(Z|X, \theta)}] \tag{20}$

前面部分，我们直接假定 $Q(Z) = P(Z|X, \theta)$ ，实际上这个后验 $P(Z|X, \theta)$ 也是难以处理的。广义EM算法思路是：

先把 $\theta$ 固定住，若Q越接近P，KL部分越小，由于 $\log P(X|\theta)$ 这时是定值，那么ELBO就会越大。即根据下式，求出 $Q(Z)$
$\hat Q(Z) = \text{argmin}_Q \ KL(Q||P) = \text{argmax}_Q \ L(Q, \theta) \tag{21}$
固定 $\hat Q(Z)$ , 就是第一步求解的值，按照求解 $\hat \theta = \text{argmax}_\theta \ L(\hat Q(Z), \theta)$ .

综上，广义EM可表示为:

E-step: $Q^{t+1} = \text{argmax}_Q L(Q, \theta^t)$
M-step: $\theta^{t+1} = \text{argmax}_\theta L(Q^{t+1}, \theta)$

对ELBO进一步化简有：

$\begin{align} L(Q, \theta) &= E_{Q}[\log\frac{ P(X, Z|\theta)}{ Q(Z)}] \\ &= E_Q[\log P(X, Z)] - E_Q[\log Q(Z)]\\ &= E_Q[\log P(X, Z)] + H[Q(Z)] \end{align} \tag{22}$

在前面的狭义EM算法中，只对 $E_Q[\log P(X, Z)]$ 进行迭代优化，是因为我们假定 $Q(Z)$ 是已知的，优化与 $H[Q(Z)]$ 部分无关。

5. EM的变种

上节介绍了广义EM算法，其中E步和M步都是求极大，也称为MM算法。这两步求解中，先固定一个参数，再优化另外一个参数；完成后，再固定优化后得到的参数，然后优化开始固定的参数，这叫做坐标上升法。SVM中求解算法SMO就是用该方法求解的。

实际过程中, $P(Z|X, \theta)$ 会采用变分推断(Variable Inference)或MCMC，结合EM算法就变成了VBEM(Variable Bayes)/VEM 和MCEM。

总结：

狭义EM算法：迭代求解算法目标式即极大似然函数 $L(\theta)$ 的下界ELBO:

$\theta^{t+1} =\text{argmax}_\theta \int_Z \log P(X, Z|\theta) P(Z|X, \theta^t) dZ\\ = \text{argmax}_\theta E_{P(Z|X, \theta^t)}[\log P(X, Z|\theta)]$
其中，E步是计算 $\log P(X,Z|\theta)$ 在概率分布 $P(Z|X, \theta^t)$ 下的期望，M步是最大化该期望。

广义EM算法：不假定 $Q(Z)=P(Z|X, \theta)$ , KL散度部分不可忽略，求解极为困难，我们使用坐标上升法求解E步和M步：

E步，固定 $\theta$ ,最大化 $L(Q, \theta)$ ,这时得到Q

M步，固定Q，再最大化 $L(Q, \theta)$ ,得到 $\theta$ 。