机器学习-白板推导8 指数簇分布

机器学习-白板推导8 指数簇分布

1. 指数簇分布背景

指数簇分布(Exponential Family Distribution)需要满足以下形式：

$$p(x|\eta) =h(x)\exp(\eta^T\phi(x) - A(\eta)) \tag{1}$$

其中：

• $\eta$ : 自然参数(natural parameter，也叫正则参数 canonical parameter)

• $\phi(x)$ : 充分统计量（sufficient statistic）,常使用的有$\phi(x) = x$，一般是一个对样本的统计函数表示。

• 接下来会重点介绍的$A(\eta)$ 是一个对数配分函数（log partition function）。

  ​ 如$P(x| \theta) = \frac{1}{z} \hat P(x|\theta)$这里的z就是归一化因子，又叫配分函数。

  ​ 对两边同时取积分：

  ​

  $$\int_{x} P(x \mid \theta)=\int_{x} \frac{1}{z} \hat{P}(x \mid \theta) \Rightarrow 1=\int_{x} \frac{1}{z} \hat{P}(x \mid \theta) \Rightarrow z=\int_{x} \hat{P}(x \mid \theta)$$

  ​ 那么$A(\eta)$为什么叫log配分函数呢？

  $$\begin{align} P(x|\eta) &= h(x) \exp(\eta^T\phi(x)-A(\eta)) \\&=h(x) \exp(\eta^T\phi(x))\exp(-A(\eta)) \\ &=\frac{1}{\exp(A(\eta))}h(x) \exp(\eta^T\phi(x)) \end{align}$$

  又因为$P(x|\theta) = \frac{1}{z} \hat P(x|\theta)$

  所以$A(\eta) = \log z$因此$z$称为配分函数 ,$A(\eta)$称为对数配分函数。

  $\exp(−A(\eta))$ 本质上扮演了归一化常数（normalization constant）的角色，也就是确保 $p(x| \eta)$ 的和或者积分等于$1$。

如果给定$\phi(x)，h(x), A(\eta)$那么就定义了被参数$\eta$控制的一个分布簇(或者集)。改变$\eta$，我们能得到这簇中的不同分布。

指数簇分布有：

• Gaussian 分布
• 伯努利分布
• 二项分布
• 泊松分布
• Beta分布
• Dirichlet分布
• Gamma分布

指数簇分布有如下性质和应用：

性质：

1. 充分统计量

   举例来说就是，对于一些从高斯分布中抽取出来的样本$x_1, x_2, \cdots, x_n$,设其充分统计量为,

$$\phi(x)=\left(\begin{array}{c} &\sum_{i=1}^{N} x_{i} &\\ &\sum_{i=1}^{N} x_{i}^{2}& \end{array}\right)$$

​ 那么我们就可以通过这个充分统计量来计算出均值和方差，从而明确其分布。这时就可以将样本丢掉，来节省空间，对online learning有重要作用。

1. 共轭：因为贝叶斯公式中分母如下：

   ​

   $$P(z|x) = \frac{P(x|z)P(z)}{\int _zP(x|z)P(z)dz}$$

   计算积分复杂或者得到的$P(z|x)$形式复杂太难计算，因此求$E_{P(z|x)}[f(z)]$也是很困难的，所以人们想了很多办法，如近似推断(变分推断，MCMC等)都是因为上述计算难。

   共轭的概念是指给定一个特殊的似然函数$P(x|z)$的情况下，后验$P(z|x)$与先验$P(z)$会有一个形式相同的分布，这就解决了上述积分困难的问题，避免求分母的积分项，在后验概率正比于似然 × 先验概率概念下有如$\underbrace{P(z \mid x)}_{\text {Beta }} \propto \underbrace{P(x \mid z)}_{\text {二项式分布 }} \underbrace{P(z)}_{\text {Beta }}$。

2. 最大熵

   ​ 最大熵原理：

   当给定一个限制条件的情况下，对于未知部分，我们假设它们等可能发生，但我们无法定量分析。而熵可以进行定量分析，我们去求解最大熵，熵越大则随机性越强。

   无信息先验：

   在贝叶斯估计中，我们往往需要给先验一个参数，有如下方法：

   ①共轭：为了计算方便

   ②利用最大熵思想：从最大熵的角度给予先验的参数（无信息先验）

   ③Jeffreys’s prior

2. 高斯分布指数簇形式

将高斯分布转换成式1指数簇这种形式：

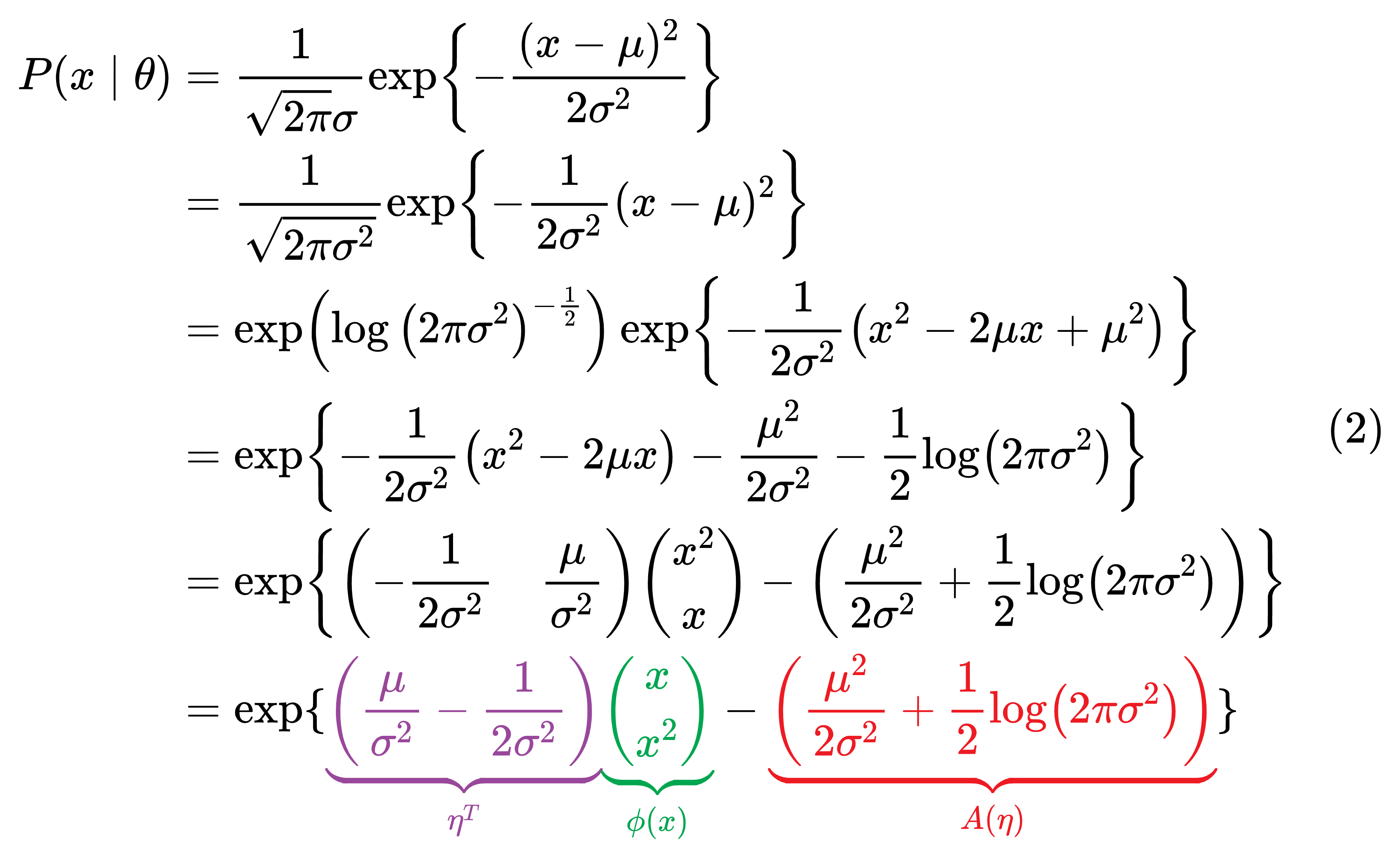
由式2中我们可以得到$\phi(x), \eta$两个式子：

$$\begin{align} &\phi(x) = \left(\begin{array}{l} x \\ x^2 \end{array}\right)\\ &\eta=\left(\begin{array}{l} \eta_{1} \\ \eta_{2} \end{array}\right)=\left(\begin{array}{c} \frac{\mu}{\sigma^{2}} \\ -\frac{1}{2 \sigma^{2}} \end{array}\right) \end{align} \tag{3}$$

现在$A(\eta)$也要用$\eta$来表示，由式3可得：

$$\sigma^2 = -\frac{1}{2\eta_2} \quad \quad \mu = -\frac{\eta_1}{2\eta_2} \tag{4}$$

式4代入到$A(\eta)$有：

$$A(\eta) = -\frac{\eta_1^2}{4\eta_2} +\frac{1}{2}\log(-\frac{\pi}{\eta_2}) \tag{5}$$

现在就得到了高斯分布的指数簇形式：

$$p(x|\eta) = \exp (\eta^T\phi(x)-A(\eta)) \tag{6}$$

更进一步来理解指数簇表示就是：$e$的指数形式的表示，其中前半部分$\exp(\eta^T\phi(x))$是一个参数和对于该分布的充分统计量，后半部分$\exp(-A(\eta))$就是再减去一个对数配分函数，并且在1小节中，我们知道如果将其转换到指数外面就是除以一个配分函数，实际上，后半部分本质上是一个归一化因子。

3. 对数配分函数与充分统计量的关系

按照式1中指数簇分布表示有：

$$\begin{align} &p(x|\eta) = h(x) \exp (\eta^T\phi(x)-A(\eta)) = \frac{h(x) \exp (\eta^T\phi(x))}{\exp(A(\eta))}\\ &\Longrightarrow p(x|\eta)\exp(A(\eta)) = h(x) \exp (\eta^T\phi(x))\\ &\Longrightarrow \int p(x|\eta)\exp(A(\eta)) dx = \int h(x) \exp (\eta^T\phi(x))dx \\ &\because \int p(x|\eta) dx = 1 \\ &\Longrightarrow \exp(A(\eta)) =\int h(x) \exp (\eta^T\phi(x))dx \end{align} \tag{7}$$

对式7两边变量$\eta$求导得:

$$\begin{align} &\frac{\partial \exp(A(\eta))}{\partial \eta} = \frac{\int h(x) \exp (\eta^T\phi(x))dx}{\partial \eta}\\ &\Longrightarrow \exp(A(\eta)) A^\prime(\eta) = \int h(x) \exp (\eta^T\phi(x))\phi(x)dx\\ &\Longrightarrow A^\prime(\eta) = \frac{\int h(x) \exp (\eta^T\phi(x))\phi(x)dx}{\exp(A(\eta))}\\ &\Longrightarrow A^\prime(\eta) = \int h(x) \exp (\eta^T\phi(x)-A(\eta))\phi(x)dx\\ &\Longrightarrow A^\prime(\eta) = \int p(x|\eta) \phi(x)dx\\ &\Longrightarrow A^\prime(\eta) = E_{p(x|\eta)} [\phi(x)] \end{align} \tag{8}$$

那么就得到了对数配分函数$A(\eta)$和充分统计量的关系：

$$A^\prime(\eta) = E_{p(x|\eta)} [\phi(x)] = \int p(x|\eta) \phi(x)dx\tag{9}$$

继续对式9中的$\eta$求导得：

$$\begin{align} A^{\prime \prime}(\eta)&=\frac{\partial\left(\int h(x) \exp \left\{\eta^{T} \phi(x)-A(\eta)\right\} \phi(x) \mathrm{d} x\right)}{\partial \eta} \\ &=\int {\color{Red}\underbrace{h(x) \exp \left\{\eta^{T} \phi(x)-A(\eta)\right\}}_{P(x \mid \eta)}}\left(\phi(x)-A^{\prime}(\eta)\right) \phi(x) \mathrm{d} x \\ &=\int P(x \mid \eta)\left(\phi(x)-E_{P(x \mid \eta)}[\phi(x)]\right) \phi(x) \mathrm{d} x \\ &=\int P(x \mid \eta) \phi^{2}(x)-E_{P(x \mid \eta)}[\phi(x)] P(x \mid \eta) \phi(x) \mathrm{d} x \\ &=\int P(x \mid \eta) \phi^{2}(x) \mathrm{d} x-E_{P(x \mid \eta)}[\phi(x)] \int P(x \mid \eta) \phi(x) \mathrm{d} x \\ &=E_{P(x \mid \eta)}\left[\phi^{2}(x)\right]-E_{P(x \mid \eta)}^{2}[\phi(x)] \\ &=\operatorname{Var}_{P(x \mid \eta)}[\phi(x)] \end{align} \tag{10}$$

由于方差不为负，所以$A(\eta)$是凸函数。

---

使用第2小节高斯分布来验证：

$$\begin{align} \sigma^2 = -\frac{1}{2\eta_2} \quad \quad \mu = -\frac{\eta_1}{2\eta_2} \\ A(\eta) = -\frac{\eta_1^2}{4\eta_2} +\frac{1}{2}\log(-\frac{\pi}{\eta_2}) \end{align}$$

直接可证明：

$$E(\phi(x))= \left[\begin{array}{cc} E(x) \\ E(x^2) \end{array}\right]= \left[\begin{array}{cc} \mu \\ \mu^2+\sigma^2 \end{array}\right]$$

因为$E(x^2) = E(x)^2+Var(x)= \mu^2+\sigma^2$,关于方差期望公式。

而我们对$A(\eta)$中$\eta$求导可得:

$$\begin{align} \frac{\partial A(\eta)}{\partial \eta_1} &= -\frac{\eta_1}{2\eta_2} = \mu \\ \frac{\partial A(\eta)}{\partial \eta_2}&= \frac{\eta_1^2}{4\eta_2^2} - \frac{1}{2\eta_2} = \mu^2 + \sigma^2 \end{align}$$

这就验证了式8和式10，我们可以看到对数配分函数的一阶导就是充分统计量量中的期望，二阶导就是方差。

---

4. 极大似然估计与充分统计量

若我们有数据集$D$如下：

$$D = \{x_1, x_2, \cdots, x_n \}$$

那么我们可以用极大似然估计来估计:

$$\begin{align} \eta_{MLE} &= \text{argmax}_\eta \ \log P(D|\eta)\\ &= \text{argmax}_\eta \ \log \prod_{i=1}^N p(x_i|\eta)\\ &= \text{argmax}_\eta \ \sum_{i=1}^N \log p(x_i|\eta)\\ &= \text{argmax}_\eta \ \sum_{i=1}^N \log \{h(x_i) \exp [\eta^T\phi(x_i)-A(\eta)] \}\\ &= \text{argmax}_\eta \ \sum_{i=1}^N \{\log h(x_i) + \eta^T\phi(x_i)-A(\eta) \} \quad \text{与}\eta\text{无关项可忽略} \\ &= \text{argmax}_\eta \ \sum_{i=1}^N [\eta^T\phi(x_i)-A(\eta)] \end{align} \tag{11}$$

对式11最后一步求导得：

$$\begin{align} &\sum_{i=1}^N [\phi(x_i) - A^{\prime}(\eta)] =0 \\ \Longrightarrow &A^{\prime}(\eta_{MLE}) = \frac{1}{N}\sum_{i=1}^N \phi(x_i) \end{align} \tag{12}$$

那么$\eta_{MLE}$就可以通过求反函数来实现。这也说明$\phi(x)$就是充分统计量，我们得到$\frac{1}{N}\sum_{i=1}^N \phi(x_i)$ 就可以求出$\eta$,进一步就得到所有的需要统计参数。

5. 最大熵

在信息论中，信息量就是概率的导数取对数，即$-\log p(x)$。熵就是对信息量的期望，因此，

$$\begin{align} H[p(x)] &= E_{p(x)}[-\log p(x)] \\&= \int -p(x)\log p(x) dx \quad \quad 连续 \\&= -\sum_{i=1}^{N}p(x_i) \log p(x_i) \quad \quad 离散 \end{align} \tag{13}$$

我们先看看离散变量的最大熵：

对于离散变量要求其熵最大，即：

$$\begin{align} \max H[p(x)] &= \max -\sum_{i=1}^{N}p_i \log p_i \\ &s.t. \quad \sum_{i=1}^N p_i= 1 \end{align} \tag{14}$$

用拉格朗日乘执法求解：

$$\text{argmin } L(p_i, \lambda) = \sum_{i=1}^{N}p_i \log p_i + \lambda(1 - \sum_{i=1}^N p_i) \tag{15}$$

对$p_i$求导得：

$$\frac{\partial L}{\partial p_i} = \log p_i + p_i \frac{1}{p_i} - \lambda = 0$$

那么$\hat p_i = \exp (\lambda -1)$. 其总和概率为1，因此离散概率分布是均匀分布且$\hat p_1 = \hat p_2 = \cdots = \hat p_k = \frac{1}{k}$.

从上述推导中看出，在离散随机变量中，均匀分布熵最大。即正在没有任何已知约束的情况下，均匀分布会使得熵最大。

最大熵原理：

上面是没有任何已知信息情况下最大熵的推导，结果是要满足均匀分布。若我们已知数据集呢？比如数据集D：

$$D = \{ x_1, x_2, \cdots, x_N\} \tag{16}$$

然后根据数据我们可以得到其经验分布：

$$\hat p(x= n) = \hat p(n) = \frac{\text{count}(n)}{N} \tag{16}$$

接下来我们就可以得到其期望$E_{\hat p } [x]$, 方差$\text{Var}_{\hat p} [x]$, ….。把情况一般化，变量$x$推广到函数向量，如：

$$\begin{aligned} &E_{\hat{p}}[\mathbf{f}(x)] =\mathbf{\Delta} \\ &\text { 其中 } \mathbf{f}(x)=\left(\begin{array}{c} f_{1}(x) \\ f_{2}(x) \\ \vdots \\ f_{Q}(x) \end{array}\right) & \mathbf{\Delta}=\left(\begin{array}{c} \Delta_{1} \\ \Delta_{2} \\ \vdots \\ \Delta_{Q} \end{array}\right) \end{aligned} \tag{17}$$

其中，$\mathbf{\Delta}$是假定的已知量。

现在，我们就可以在满足上述条件下，求其最大熵，这个优化问题如下：

$$\left\{\begin{array}{c} \min \sum_x p(x) \log p(x)\\ \text {s.t. } \sum_x p(x)=1 \\ E_{p}[\mathbf{f}(x)]=E_{\hat{p}}[\mathbf{f}(x)]=\mathbf{\Delta} \end{array}\right. \tag{18}$$

用拉格朗日乘子法：

$$L(p, \lambda_o, \mathbf{\lambda_1}) = \sum_x p(x) \log p(x) + \lambda_0 (1 - \sum_x p(x)) + \mathbf{\lambda_1}^T(\mathbf{\Delta} - E_{p}[\mathbf{f}(x)]) \tag{19}$$

对每个$p(x_i)$求导， 并且$E_{p}[\mathbf{f}(x)] =\sum_x p(x_i)\mathbf{f}(x)$,那么：

$$\begin{align} \frac{\partial L}{\partial p(x)} = &\log p(x) + p(x) \frac{1}{p(x)} - \lambda_0 -\mathbf{\lambda_1}^T \mathbf{f}(x) \\ = &\log p(x) + 1 -\lambda_0 -\mathbf{\lambda_1}^T \mathbf{f}(x) \\ \Longrightarrow &\log p(x) = \lambda_0 + \mathbf{\lambda}_1^T \mathbf{f}(x) - 1 \\ \Longrightarrow &p(x) = \exp [ \mathbf{\lambda}_1^T \mathbf{f}(x) - (1 - \lambda_0) ] \end{align} \tag{19}$$

注：在求导时，只是对单独的$x_i$求导，遇到$x_j (i \neq j)$时，结果为0， 可忽略。

式19中，我们看到最大熵要求分布$p(x)$满足指数簇分布，在满足既定数据的情况下，最大熵对应着要求满足指数簇分布。

Inference

[1] 最大熵模型理论及NLP应用总结

[2] “共轭分布”是什么？