机器学习-白板推导 7 核方法

机器学习-白板推导 7 核方法

1. 线性不可分问题

对于如下图中的异或问题，是线性不可分的。

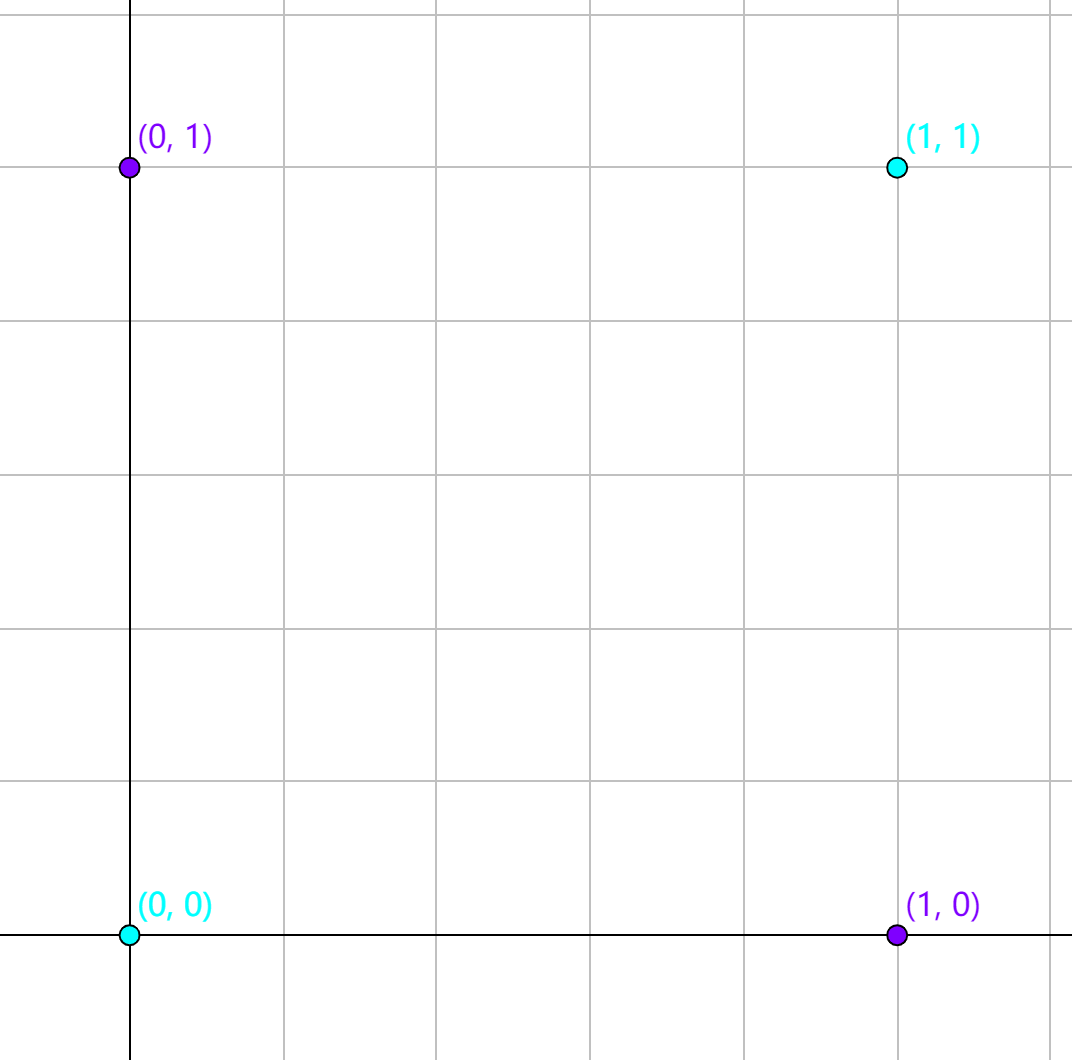
但是将数据映射到高维空间后就可以实现线性可分。如果将异或问题中的数据通过一个映射$\phi(x)$将低维空间中的数据$x$映射成高维空间中的$z$来实现数据的线性可分。如：

$$x = (x_1, x_2) \overset{\phi(x)} \Longrightarrow z=(x_1, x_2, (x_1-x_2)^2)$$

就可以得到如下数据分布：

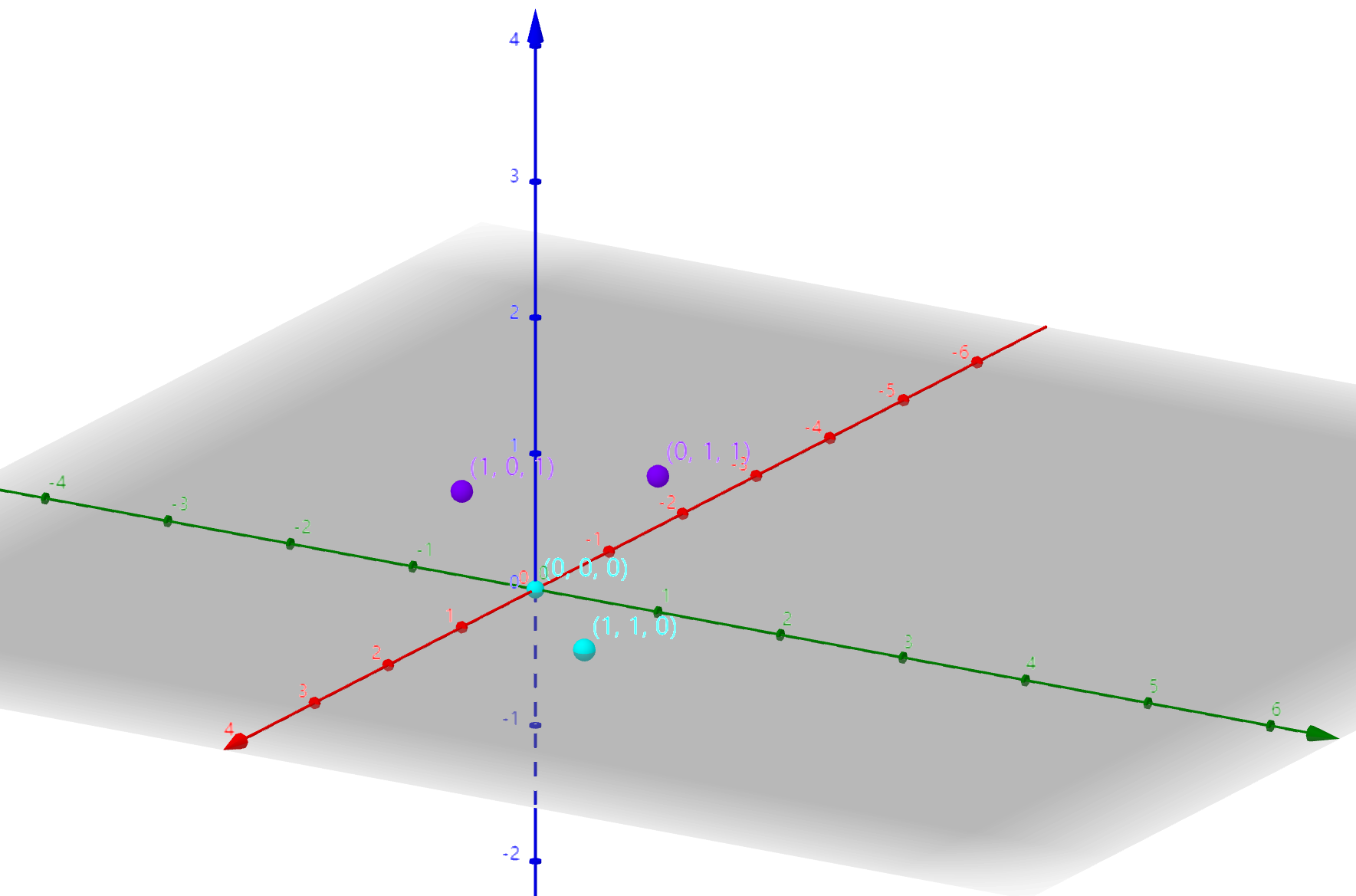
这时就可以轻松将两类点分开。

2. 核函数的引入

机器学习-白板推导6 SVM 小节3中对偶问题的拉格朗日乘子法目标函数为：

$$\begin{align} \max_{\lambda} L(\boldsymbol{w}, b, \lambda) & = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j +\sum_{i=1}^N\lambda_i \\ &\text{s.t. } \quad \lambda_i \ge 0, \quad\sum_{i=1}^N\lambda_iy_i = 0, \quad i=1, \cdots, N \end{align} \tag{1}$$

其中，含有$\boldsymbol{x}_i^T\boldsymbol{x}_j$项，如果我们定义一个映射$\phi(\boldsymbol{x})$,将低维的特征映射到高维特征空间中，将会使得数据线性可分。但是这个映射过程如果维度过高，计算量将非常大。为此引入核函数，kernel function的作用之一就是省去计算$\phi(\boldsymbol{x})$，直接得到$\phi(\boldsymbol{x})^T\phi(\boldsymbol{z})$。

核函数定义: （《统计机器学习 》P144定义）

设$\mathcal{X}$是输入空间($\mathbb{R}^n$),又设$\mathcal{H}$是希尔伯特空间，如果存在：

$$\phi(\boldsymbol{x}):\mathcal{X} \mapsto \mathcal{H} \tag{2}$$

使得对所有的$\boldsymbol{x}, \boldsymbol{z} \in \mathcal{X}$，函数$K(\boldsymbol{x}, \boldsymbol{z})$满足条件：

$$K(\boldsymbol{x}, \boldsymbol{z}) = <\boldsymbol{x}, \boldsymbol{z}> \tag{3}$$

其中$<\boldsymbol{x}, \boldsymbol{z}> = \boldsymbol{x}^T\boldsymbol{z}$就是内积，希尔伯特空间$\mathcal{H}$在下一节介绍。

例子：

$k(x,x’)=\exp(-\frac{(x-x’)^2}{2\sigma^2})$ 是一个核函数。

证明：

$$\begin{align} \exp(-\frac{(x-x')^2}{2\sigma^2})&=\exp(-\frac{x^2}{2\sigma^2})\exp(\frac{xx'}{\sigma^2})\exp(-\frac{x'^2}{2\sigma^2})\nonumber\\ &=\exp(-\frac{x^2}{2\sigma^2})\sum\limits_{n=0}^{+\infty}\frac{x^nx'^n}{\sigma^{2n}n!}\exp(-\frac{x'^2}{2\sigma^2})\nonumber\\ &=\exp(-\frac{x^2}{2\sigma^2})\varphi(x)\varphi(x')\exp(-\frac{x'^2}{2\sigma^2})\nonumber\\ &=\phi(x)\phi(x') \end{align}$$

实际上，我们一般使用的都是正定核函数。那么什么是正定核函数呢？

3. 正定核函数的两个定义

定义一：

$$\begin{align} &若存在一个映射K:\mathcal{X}\times\mathcal{X}\mapsto\mathbb{R}，并且\forall x,z \in \mathcal{X}。如果存在一个\phi:\mathcal{X}\mapsto \mathbb{R}^p，\\&并且\phi(x)\in\mathcal{H}，使得K(x,z) = <\phi(x),\phi(z)>，那么称K(x,z)为正定核函数。 \end{align} \tag{4}$$

定义二：

$$\begin{align} &对于一个映射K:\mathcal{X}\times\mathcal{X}\mapsto\mathbb{R}，对于\forall x,z\in \mathcal{X}，都有K(x,z)。 \\&如果K(x,z)满足，1. 对称性；2. 正定性；那么称K(x,z)为一个正定核函数。 \end{align} \tag{5}$$

对称性，正定性解释：

1. 对称性：$K(x, z) = K(z, x)$
2. 正定性: 任取N个元素, $x_1, x_2, \cdots, x_N \in \mathcal{X}$,其对应的Gram Matrix (也叫Kernel Matrix) $[ K(x_i, x_j)]_{n \times n}$，就是对应元素的kernel矩阵是半正定的

先介绍Hilbert Space: 希尔伯特空间是一个完备的，可能是无限维的，被赋予内积运算的线性空间。

1. 线性空间：空间中任意两个向量都可以由基向量线性表示

2. 完备的：对极限操作的封闭性。希尔伯特空间是一个函数空间，空间中每个元素都是函数，因此：

   ​

   $$\lim_{n \to +\infty} K_N = K \in \mathcal{H} \tag{6}$$

3. 内积 内积要满足3个条件：正定性， 对称性， 线性

• 对称性：$f, g \in \mathcal{H}$, 就有$<f, g> = <g, f>$,这里$f, g$都是函数。
• 正定性：$f, f \ge 0$， 只有当$f =0$ 时取等号。
• 线性：$<a_1f_1 + a_2f_2, g> = a_1<f_1, g> + a_2<f_2, g>$。

如果使用定义一，很难找到$K(x, z)$,我们一般用定义二来判断$K(x, z)$是否为正定核函数。

4. 正定核函数充要条件

问题是：

$$K(x, z) = <\phi(x), \phi(z)> \Longleftrightarrow K<x, z> 是对称半正定矩阵$$

1. 对称性：

$$\begin{equation} K(x,z)=<\phi(x),\phi(z)> \qquad K(z,x) = <\phi(z),\phi(x)> \end{equation}$$

又因为：

$$\begin{equation} <\phi(x),\phi(z)> = <\phi(z),\phi(x)> \end{equation}$$

所以$K(x,z)=K(z,x)$。

1. 正定性：令$K_{ij} = K(x_i, x_j)$有 $$\begin{align} \alpha^TK\alpha = & \begin{bmatrix} \alpha_1 & \alpha_2 & \cdots & \alpha_N \end{bmatrix} \begin{bmatrix} K_{11} & K_{12} & \cdots & K_{1N} \\ K_{21} & K_{22} & \cdots & K_{2N} \\ \vdots & \vdots & \ddots & \vdots \\ K_{N1} & K_{N2} & \cdots & K_{NN} \\ \end{bmatrix} \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_N \end{bmatrix} \\ = & \sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_jK_{ij} \\ = & \sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j<\phi(x_i),\phi(x_j)> \\ = & \sum_{i=1}^N\sum_{j=1}^N \alpha_i\alpha_j\phi(x_i)^T\phi(x_j) \\ = & \sum_{i=1}^N\phi(x_i)^T\sum_{j=1}^N\phi(x_j) \\ = & \left[ \sum_{i=1}^N\phi(x_i) \right]^T \left[ \sum_{j=1}^N\phi(x_j) \right] \\ = & \left|\left| \sum_{i=1}^N \alpha_i\phi(x_i) \right|\right|^2 \geq 0 \end{align}$$ 所有K是半正定的。

5. 非线性支持向量机

式1引入核函数就能应用到非线性分类中：

$$\begin{align} \min_{\lambda} L(\lambda) & = \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N\lambda_i\lambda_jy_iy_jK(\boldsymbol{x}_i,\boldsymbol{x}_j) -\sum_{i=1}^N\lambda_i \\ &\text{s.t. } \quad \lambda_i \ge 0, \quad\sum_{i=1}^N\lambda_iy_i\ = 0, \quad i=1, \cdots, N \end{align} \tag{7}$$

现在SVM算法选择合适的核函数$K(x, z)$就可以对非线性可分数据集分类了。

Inference

[1] 支持向量机原理(三)线性不可分支持向量机与核函数