机器学习-白板推导6 SVM 上

1.SVM 核心知识点

Support Vector Machine(SVM) 有三宝，间隔，对偶，核技巧。其分类有：

Hard-margin SVM
Soft-margin SVM
Kernel SVM

本文将介绍软硬间隔部分, 核技巧等将在下篇中介绍。

2. SVM模型引入

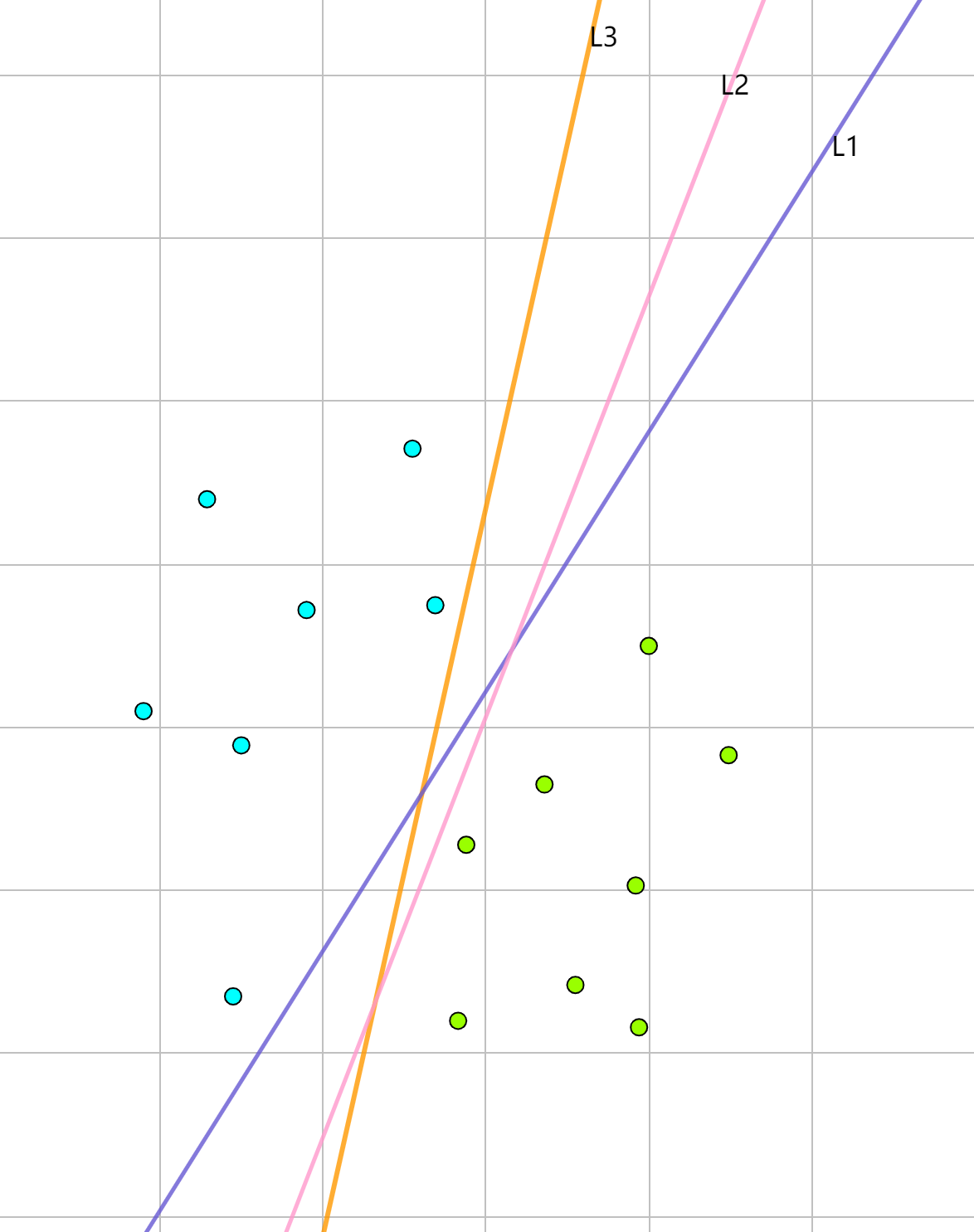
SVM模型就是找到一个超平面将两类数据点分隔开，这个超平面记为 $f(\boldsymbol{w}) = \boldsymbol{w}^Tx + b$ 。如上图所示，这样的超平面很多，如 $L_1, L_2, L_3$ ，那么哪个最好呢？直觉上，离这些点距离越远越好。间隔就是相对距离最近的点与超平面的距离，首先先将问题数学化定义。

对于数据集 $D=\{(\boldsymbol{x}_i,y_i)\}^{N}_{i=1}$ ，其中 $\boldsymbol{x}_i\in\mathbb{R}^{p}, \ y_i\in\{1,-1\}$ 。要将数据点分隔开的间隔最大化，并且要将所有点分类正确：

$\max \text{ margin} (\boldsymbol{w},b) \\ s.t. \ \left\{ \begin{array}{ll} \boldsymbol{w}^T_ix+b>0 \quad y_i = +1 \\ \boldsymbol{w}^T_ix+b<0 \quad y_i = -1 \\ \end{array} \right. \tag{1}$

因为约束条件可改写为：

$s.t. \quad y_i(\boldsymbol{w}_i^Tx + b) > 0, \quad (i=1, 2, \cdots, N) \tag{2}$

对于间隔，即样本空间点到超平面 $(\boldsymbol{w}, b)$ 的最小距离可写作：

$\begin{align} &\min \frac{1}{\lVert \boldsymbol{w} \rVert} |\boldsymbol{w}^T\boldsymbol{x}_i + b| \quad \quad (i=1, 2, \cdots, N ) \\= &\min \frac{1}{\lVert \boldsymbol{w} \rVert} y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \\=&\frac{1}{\lVert \boldsymbol{w} \rVert} \min\ y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \end{align} \tag{3}$

进一步简化问题，式2中约束是 $y_i(\boldsymbol{w}_i^Tx + b) > 0$ ,那么 $\exists \gamma \gt 0, \ 令\min\ y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) = \gamma$ 。这时最小间隔就是 $\gamma$ ，对于所有点都应该大于等于最小间隔， $y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \ge \gamma$ 。目标函数整理后：

$\max_{\boldsymbol{w}, b} \frac{\gamma}{\lVert \boldsymbol{w} \rVert } \quad \quad s.t. \quad y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \ge \gamma \tag{4}$

但是有个问题 $\gamma$ 是函数间隔，就是 $\boldsymbol{w}， b$ 放大为2倍时，函数间隔也会扩大。因此要约束。不妨令 $\gamma = 1$ , 并且这时式4中 $\max_{\boldsymbol{w}, b} \frac{1}{\lVert \boldsymbol{w} \rVert }$ 等价于 $\min_{\boldsymbol{w}, b} \frac{1}{2}\lVert \boldsymbol{w} \rVert ^2 = \min_{\boldsymbol{w}, b} \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w}$ （最大导数变为最小其互导数，并且为了简化计算改写下）。这时目标函数改写为：

$\left \{ \begin{array}{ll} \min_{\boldsymbol{w}, b} \ \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w}\\ \text{s.t} \quad y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \ge 1, \quad i=1, \cdots, N \end{array} \right. \tag{5}$

3. SVM 模型求解(硬间隔)

上节中式5 是带约束的优化问题，可以用拉格朗日乘子法来求解。

其拉格朗日函数为：

$L(\boldsymbol{w}, b, \lambda) = \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + \sum_{i=1}^{N} \lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)) \tag{6}$

其中 $\lambda_i \ge 0$ . 如果其等于0，就没有约束条件了，变为直接取最小值。

关于 $\lambda_i \gt 0$ 原因：因为要目标函数的梯度和可行域的梯度要平行且同向， $-\nabla_{\boldsymbol{x}}f(x) = \lambda \nabla_{\boldsymbol{x}}g(x) \quad 且 \lambda \gt 0$ 。如果小于0，就反向了。

具体看这个KKT。

那么式6和式5约束问题为什么等价呢？

令 $\Delta =1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)$ 有：

若 $\Delta \gt 0$ ,那么 $\sum_{i=1}^{N} \lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b))$ 将取到无穷大，所以 $\max_{\lambda} L(\boldsymbol{w}, b, \lambda) = \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + \infty =\infty$
若 $\Delta \le 0$ , 当 $\lambda_i = 0$ 时, 则 $\sum_{i=1}^{N} \lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b))$ 取最大值0，因此 $\max_{\lambda} L(\boldsymbol{w}, b, \lambda) = \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + 0=\frac{1}{2} \boldsymbol{w}^T\boldsymbol{w}$

综上所述， $\min_{\boldsymbol{w}, b} \max_{\lambda} L(\boldsymbol{w}, b, \lambda) = \min_{\boldsymbol{w}, b} \{\infty, \ \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w}\}$ 将取 $\frac{1}{2} \boldsymbol{w}^T\boldsymbol{w}$ 。这样隐式地保证了 $\Delta =1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \le 0$ 来满足约束条件。

现在原问题：

$\left \{ \begin{array}{ll} \min_{\boldsymbol{w}, b } \max_{\lambda } \ L(\boldsymbol{w}, b, \lambda) \\ \text{s.t} \quad \lambda_i \ge 0 \end{array} \right. \tag{7}$

将其转化为对偶问题是：

$\left \{ \begin{array}{ll} \max_{\lambda } \min_{\boldsymbol{w}, b } \ L(\boldsymbol{w}, b, \lambda) \\ \text{s.t} \quad \lambda_i \ge 0 \end{array} \right. \tag{8}$

简单介绍下对偶问题，具体看《统计学习方法》 P448。

式7中拉格朗日乘子法的极小极大问题的对偶问题是极大极小问题。

并满足 $\min \max L \ge \max \min L$ ，因为对于该不等式， $\min \max L$ 最优解在最大值里面取最小的，而 $\max \min L$ 是最小值里面取最大的。类似于“宁为鸡头不为凤尾”。

弱对偶关系就是： $\min\max \geq \max\min L$ 。

强对偶关系就是： $\min\max L = \max\min L$ 。

求解参数值：

对于目标函数 (转换为求解其对偶问题):

$\max_{\lambda} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \lambda) = \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + \sum_{i=1}^{N} \lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b)) \quad \quad i=1, \cdots, N \tag{9}$

简化下方便计算：

$\begin{align} L(\boldsymbol{w},b,\lambda) = & \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w} + \sum_{i=1}^N\lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) \\ = & \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w} + \sum_{i=1}^N\lambda_i - \sum_{i=1}^N\lambda_iy_i\boldsymbol{w}^T\boldsymbol{x}_i - \sum_{i=1}^N\lambda_iy_ib \\ \end{align} \tag{10}$

对参数 $b$ 求导：

$\frac{\partial L}{\partial b} = -\sum_{i=1}^N\lambda_iy_i \tag{11}$

对参数 $\boldsymbol{w}$ 求导，先将式11代入式10，然后求导。

$L(\boldsymbol{w},b,\lambda) = \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w} + \sum_{i=1}^N\lambda_i - \sum_{i=1}^N\lambda_iy_i\boldsymbol{w}^T\boldsymbol{x}_i \tag{12}$

对其求导得：

$\frac{\partial L}{\partial \boldsymbol{w}} = \boldsymbol{w} -\sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i = 0 \tag{13}$

这里 $\boldsymbol{w}^\star = \sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i$ 是样本数据的线性组合。

求解 $\min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \lambda)$ , 依旧将 $\boldsymbol{w}^\star$ 代入式12得：

$\begin{align} \min_{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \lambda) &= \frac{1}{2} (\sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i)^T\sum_{j=1}^N\lambda_jy_j\boldsymbol{x}_j +\sum_{i=1}^N\lambda_i - \sum_{i=1}^N\lambda_iy_i(\sum_{j=1}^N\lambda_jy_j\boldsymbol{x}_j)^T\boldsymbol{x}_i \\ &= -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j +\sum_{i=1}^N\lambda_i \end{align} \tag{14}$

现在问题简化为：

$\begin{align} \max_{\lambda} L(\boldsymbol{w}, b, \lambda) & = -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j +\sum_{i=1}^N\lambda_i \\ &\text{s.t. } \quad \lambda_i \ge 0, \quad\sum_{i=1}^N\lambda_iy_i = 0, \quad i=1, \cdots, N \end{align} \tag{15}$

4. SVM KKT条件导出

KKT条件实际上由以下部分构成：

目标函数和所有约束条件组成的拉格朗日函数的梯度为0。
互补松弛条件（complementary slackness），就是不等式约束和其拉格朗日系数积为0。
不等式约束条件
等式约束条件
拉格朗日系数约束

其中，互补松弛条件解释跟小节3中 $\lambda_i \ge 0$ 部分类似，还可以看看关于这个得解释拉格朗日乘子法 - KKT条件 - 对偶问题。

导出式15的KKT条件为：

$\begin{equation} \left\{ \begin{array}{ll} \frac{\partial L}{\partial \boldsymbol{w}} = 0,\quad \frac{\partial L}{\partial b} = 0,\quad \frac{\partial L}{\partial \lambda} = 0 & \\ \lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) = 0 & \\ 1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \leq 0 &\\ \lambda_i \geq 0 & \\ \end{array} \right. \end{equation} \tag{16}$

其中式16中第二排等式就是互补松弛条件。满足KKT条件是原问题的对偶问题具有强对偶关系的充分条件，当然也包括目标函数 $f(x)$ 和不等式约束为凸函数，等式约束为仿射函数这些必备条件。

根据小节3中， $\boldsymbol{w}^\star = \sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i$ 。

那么 $b^{\star}$ 呢？这时使用互补松弛条件来求解， $\lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) = 0$ 。

再解释下具体SVM中这个条件是怎么来的。如下图，图来自于 Wiki SVM

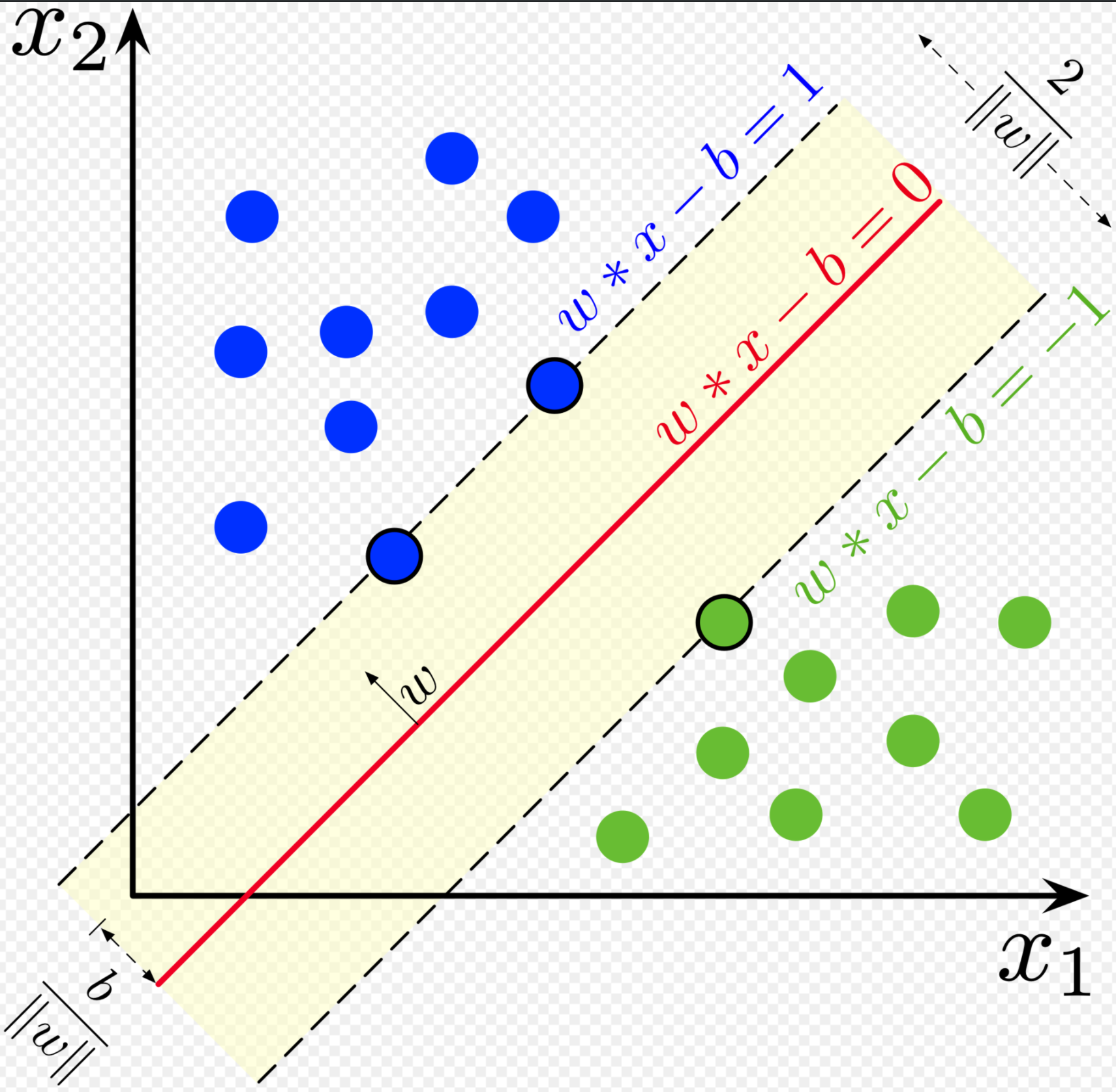
图中距离分割超平面最近的点都落在 $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) = \pm 1$ 上，这些点叫支持向量。SVM算法最核心部分就是找支持向量。

对于支持向量，必然有 $1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=0$ ，那么 $\lambda_i(1-y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) = 0$ 中 $\lambda_i$ 才有可能取值( $\lambda_i \neq 0$ )。其它点的话， $\lambda_i = 0$ 。

不妨假设一个支持向量为 $(\boldsymbol{x}_k, y_k)$ 那么，

$\begin{align} &1-y_k(\boldsymbol{w}^T\boldsymbol{x}_k+b)=0 \\ &\Longrightarrow y_kb^{\star} = 1-y_k\boldsymbol{w^{\ast ^T}}\boldsymbol{x}_k\\ &\Longrightarrow b^{\star} = y_k-\boldsymbol{w^{\ast ^T}}\boldsymbol{x}_k \quad \quad 因为y_k= \pm 1 \\ & \Longrightarrow b^{\star} = y_k -\sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i\boldsymbol{x}_k \end{align} \tag{17}$

总结：

到此为止，我们求出了硬间隔的SVM的最优解，模型为：

$f(\boldsymbol{x}) = \text{sign }(\boldsymbol{w^{\ast ^T}}\boldsymbol{x} + b^{\star} ) \tag{18}$

其中， $\boldsymbol{w}^\star = \sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i, \quad b^{\star} = y_k -\sum_{i=1}^N\lambda_iy_i\boldsymbol{x}_i\boldsymbol{x}_k$

并且KKT条件是原问题的对偶问题有强对偶关系的充要条件，利用支持向量求解SVM计算相对简单。支持向量寻找过程是通过代入数据点，从满足式15中当 $\lambda_i=0$ 时，对应数据点就是是支持向量。具体计算算法看SVM SMO这节。

5. SVM 软间隔

上面介绍的SVM要求数据集能完全被分开，不能有数据点噪声落在硬间隔区间内，但是数据集必然有噪声等落在这个区间。Soft Margin就是允许一些点落在margin内。

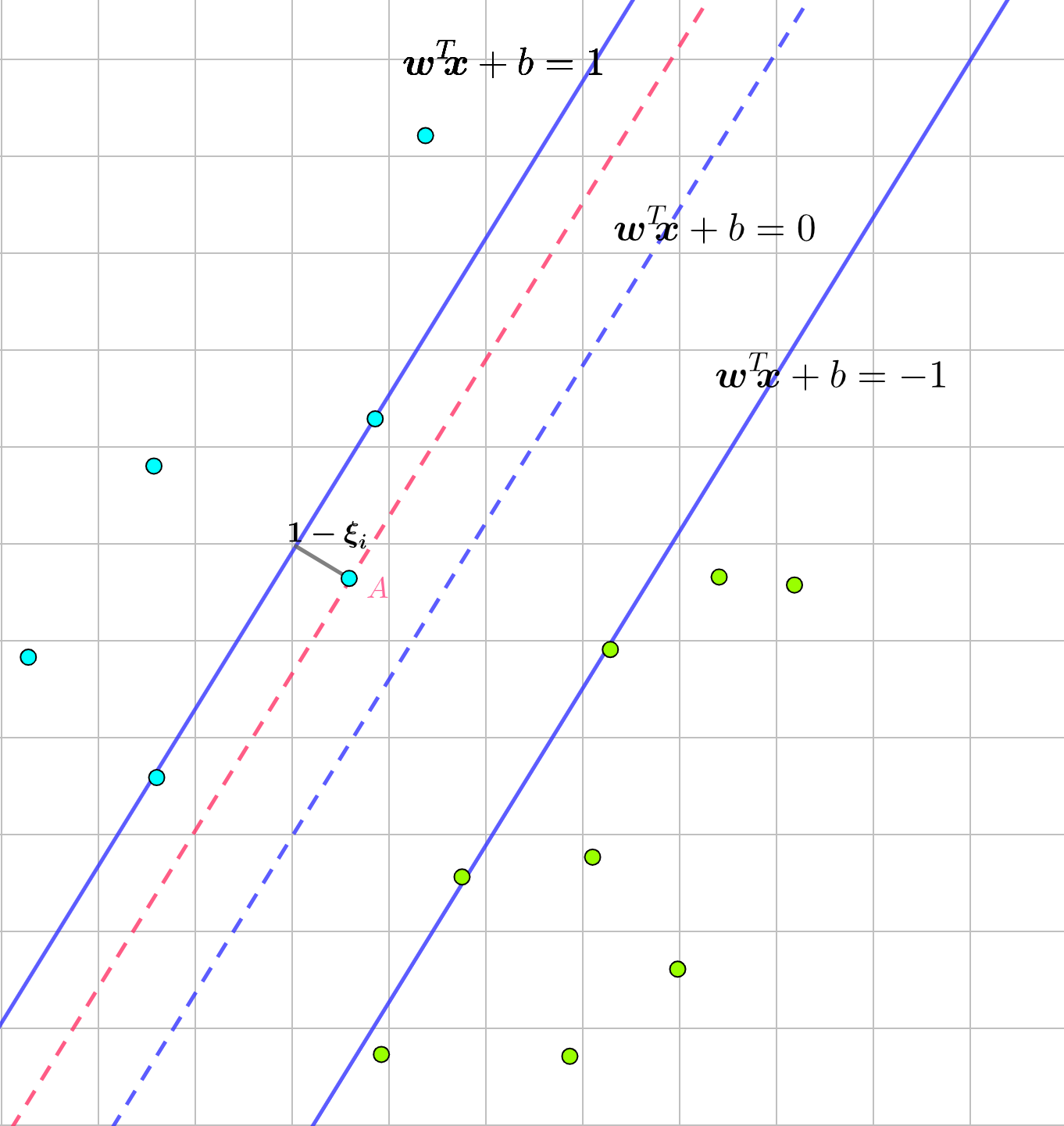
如上图中，对于要分类的两类数据点，落入蓝色实线之间的点就是被误分类的，图中A点，那么 $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \lt 1$ 。如果有多个呢？我们引入指示函数有：

$\text{loss} =\sum_{i=1}^{N} I \{y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)) \lt 1\}$

其中 $I$ 是指示函数，不连续，不可导。

不妨将其转换为距离来看损失函数。

若 $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \ge 1$ ,正确分类，损失为0
若 $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \lt 1$ ，距离为图中 $\epsilon$ , $1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)$

用max来合并下这些距离， $\text{loss} = \max\{0, 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\}$ ，这个函数叫hinge loss。

现在式5，加上合页损失就是目标函数：

$\left \{ \begin{array}{ll} \min_{\boldsymbol{w}, b} \ \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + C\sum_{i=1}^N \max\{0, 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)\}\\ \text{s.t} \quad y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \ge 1, \quad i=1, \cdots, N \end{array} \right. \tag{19}$

其中，C是惩罚系数，有点像正则化中的系数。

令 $\xi_i = 1 - y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)$ , 因为其是距离 $\xi_i \ge 0$ 。式19就可以简化为：

$\left \{ \begin{array}{ll} \min_{\boldsymbol{w}, b} \ \frac{1}{2} \boldsymbol{w}^T\boldsymbol{w} + C\sum_{i=1}^N \xi_i \\ \text{s.t} \quad y_i(\boldsymbol{w}^T\boldsymbol{x}_i + b) \ge 1-\xi_i, \quad \xi_i \ge 0, \ i=1, \cdots, N \end{array} \right. \tag{20}$

如上图中， $1- \xi_i$ 就是允许误分类点到分类边界的距离，也可以认为是允许误分类点的范围。接下来也可以用拉格朗日乘子法求解。