机器学习-白板推导 3. 线性回归

机器学习-白板推导 3. 线性回归

1. 线性回归矩阵表示

假定数据集：

$$\mathcal{D}=\{(x_1, y_1),(x_2, y_2),\cdots,(x_N, y_N)\}, \ 其中x_i\in\mathbb{R}^{p}，y_i\in\mathbb{R}，i=1, \ 2,\cdots,\ N。$$

数据矩阵为：(这样可以保证每一行为一个数据点)

$$\begin{equation} X=(x_1, x_2, \cdots, x_N)^T= \begin{pmatrix} x_1^T \\ x_2^T \\ \vdots\\ x_N^T \\ \end{pmatrix} = \begin{pmatrix} x_{11} & x_{12} & \dots & x_{1p}\\ x_{21} & x_{32} & \dots & x_{2p}\\ \vdots & \vdots & \ddots & \vdots\\ x_{N1} & x_{N2} & \dots & x_{Np}\\ \end{pmatrix}_{N\times P} \end{equation}$$ $$\begin{equation} Y= \begin{pmatrix} y_1 \\ y_2 \\ \vdots\\ y_N \\ \end{pmatrix}_{N\times 1} \end{equation}$$

设拟合的函数为：$f(x)=W^T x$

如下图所示，

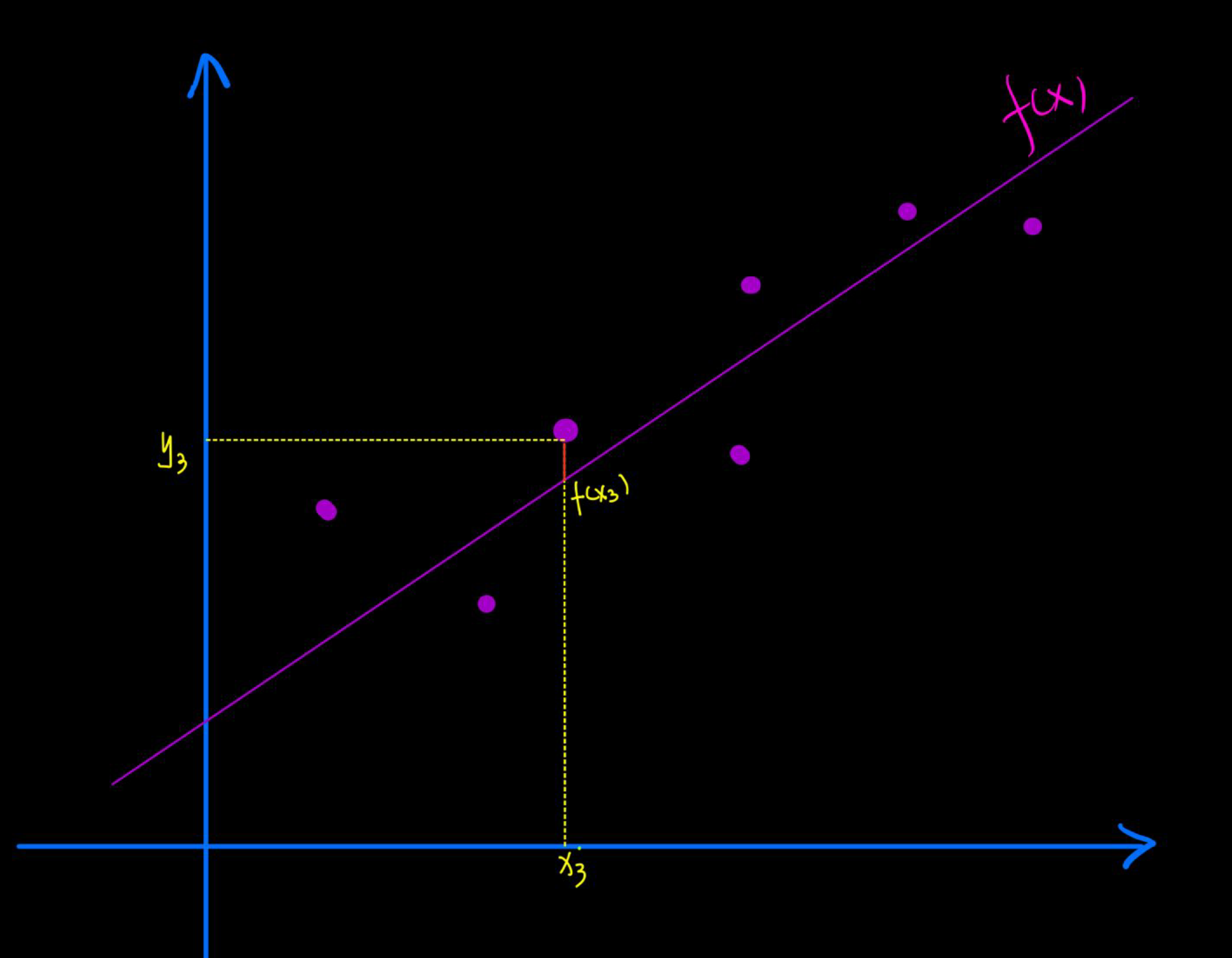
对于每个样本点，比如$(x_3, y_3)$的残差就是红色部分的距离：$\lVert w^Tx_3 - y_3 \rVert^2$.因此总的损失为：

$$\begin{align} L(w) = & \sum_{i=1}^{N}\lVert w^T x_i-y_i\rVert^2 \\ = & (w^T x_1-y_1, w^T x_2-y_2, \dots, w^T x_N-y_N) \begin{pmatrix} w^T x_1-y_1\\ w^T x_2-y_2\\ \vdots\\ w^T x_N-y_N\\ \end{pmatrix} \end{align}$$

写成矩阵形式就是：

$$\begin{align} L(W) = & (W^TX^T-Y^T)(W^TX^T-Y^T)^T \\ = & (W^TX^T-Y^T)(XW-Y) \\ = & W^TX^TXW - W^TX^TY - Y^TXW + Y^TY\\ = & W^TX^TXW - 2W^TX^TY + Y^TY \end{align}$$

对 $W$求导得：

$$\frac{\partial L(W)}{\partial W} = 2X^TXW-2X^TY = 0 \Longrightarrow W=(X^TX)^{-1}X^TY$$

这里要求$（X^TX）^{-1}$满秩，也就是$X^TX \in \mathbb{R}^{p \times p}$是满秩的即$X$矩阵列向量都是独立的，即$X$特征列都不相关。

2. 最小二乘估计的几何意义

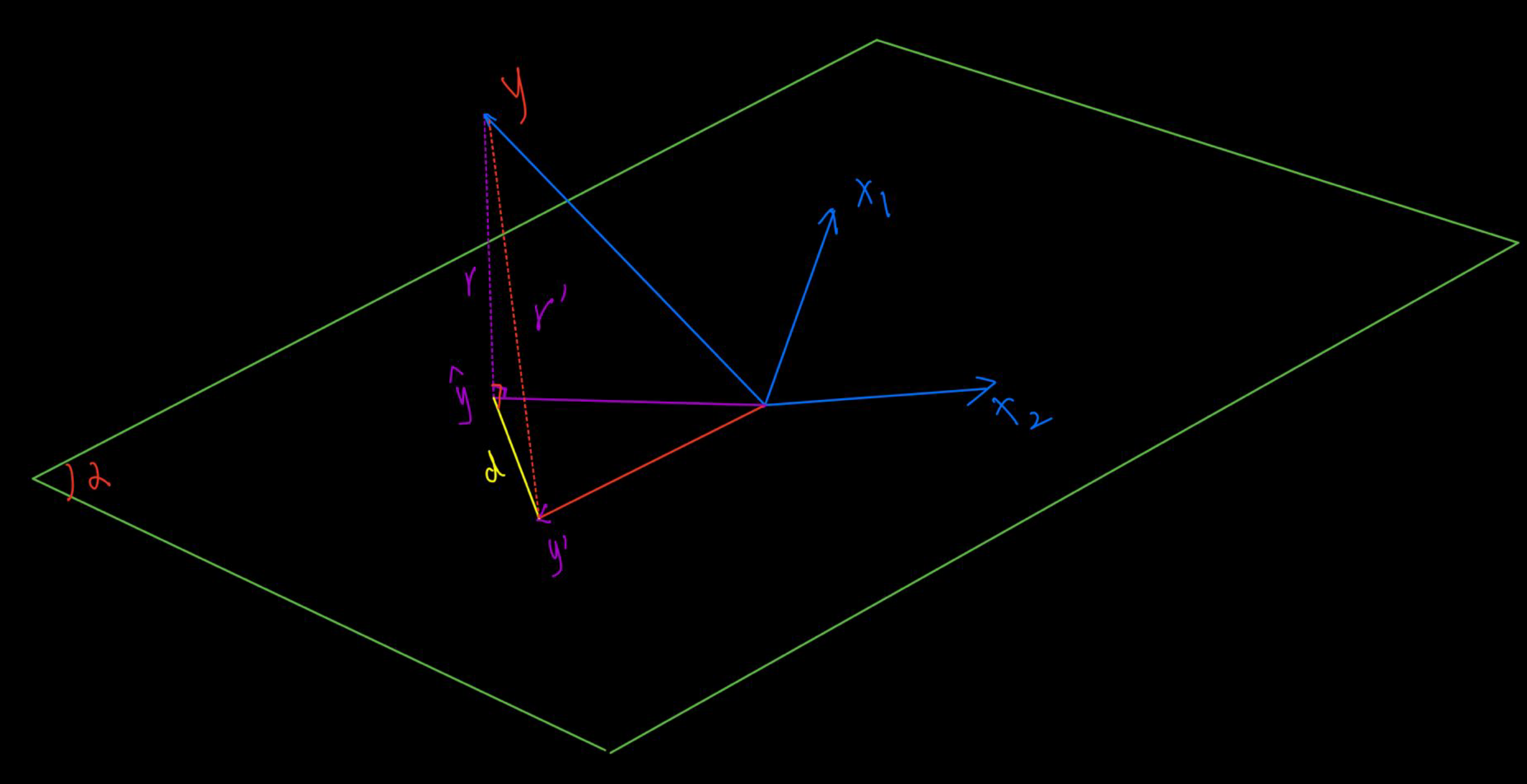
如上图，假设样本$\mathbf{x}_1, \mathbf{x}_2$张成空间为平面$\alpha$。 那么其通过拟合得到的函数为:

$$\hat {\mathbf{y}}= w_1x_i + w_2x_2$$

当我们拟合得到的$\hat {\mathbf{y}}$正好是真实值$\mathbf{y}$在平面$\alpha$内的投影时，可以使得d最小。即$r \perp 平面\alpha$那么有：

$$X^T(Y - X^TW) = 0$$

因此$W = (X^TX)^{-1}X^TY$.

3. 从概率视角看最小二乘法

假设$\mathbf{y} = \mathbf{w}^T\mathbf{x} + \mathbf{\epsilon}$, 其中$\mathbf{\epsilon} \sim \mathcal{N}(0, \sigma^2)$。那么有$\mathbf{y} \sim \mathcal{N}(\mathbf{w}^T\mathbf{x} , \sigma^2)$。在该条件下，目标是求$\mathbf{w}$使得观察值$\mathbf{y}$出现的概率最大，使用MLE求解下式：

$$P(y|x;w)=\frac{1}{\sqrt{2\pi}\sigma} \text{ exp}\left(-\frac{(y-w^Tx)^2}{2\sigma^2}\right)$$

即对于每个样本$\mathbf{x}_i$都能式上面概率最大：

$$\begin{align} L(w) = & \text{ ln}\ p(y|x;w) = \text{ ln}\prod_{i=1}^Np(y_i|x_i;w) \\ = & \sum_{i=1}^N\text{ ln}\ p(y_i|x_i;w) \\ = & \sum_{i=1}^N \left( \text{ ln}\frac{1}{\sqrt{2\pi}\sigma} + \text{ ln}\ \text{ exp}\left( -\frac{(y_i - w^Tx)^2}{2\sigma^2} \right) \right)\\ = &\sum_{i=1}^N \left( \text{ ln}\frac{1}{\sqrt{2\pi}\sigma} + -\frac{(y_i - w^Tx)^2}{2\sigma^2} \right) \end{align}$$

因此，只要$(y_i - w^Tx)^2$最大即可。这与矩阵求解表达式一样，因此，最小二乘法隐含着一个条件，噪声符合高斯分布。

4. 正则化

对损失函数正则化后，表达式变为$L(w)+\lambda P(w)$。

1. Lasso，其中$P(w) = \lVert w \rVert_1 = \sum_{i=1}^Nw_i$
2. Ridge，岭回归，也就是$P(w)=\lVert w\lVert_2^2=\sum_{i=1}^Nw_i^2$

岭回归频率派角度

损失函数改写为 $L(W)=\sum_{i=1}^N\lVert w^Tx_i-y_i \rVert^2 + \lambda W^TW$

$$\begin{align} L(W) = & \sum_{i=1}^N \lVert w^Tx_i-y_i \rVert^2 + \lambda W^TW \\ \nonumber = & (W^TX^T - Y^T)(XW-Y)+\lambda W^TW \\ \nonumber = & W^TX^TXW - W^TX^TY - Y^TXW - Y^TY + \lambda W^TW \\ \nonumber = & W^TX^TXW - 2W^TX^TY - Y^TY + \lambda W^TW \\ \nonumber = & W^T(X^TX + \lambda I)W - 2W^TX^TY - Y^TY \end{align}$$

然后 $L(W)$对$W$求导得：

$$\frac{\partial J(W)}{\partial W} = 2(X^TX + \lambda I)W - 2X^TY = 0$$

可得：

$$W = (X^TX + \lambda I)^{-1}X^TY$$

这里，因为$X^T X$是半正定矩阵, $X^TX + \lambda I$必然可逆。

岭回归Bayes估计角度

根据第3小节所说， $\mathbf{\epsilon} \sim \mathcal{N}(0, \sigma^2)，\ \mathbf{y} \sim \mathcal{N}(\mathbf{w}^T\mathbf{x} , \sigma^2)$ 可以得到 $P(w), P(y|w)$:

$$P(y|w) = \frac{1}{\sqrt{2\pi}\sigma} \text{ exp}\left( -\frac{(y - w^Tx)^2}{2\sigma^2} \right) \\ P(w) = \frac{1}{\sqrt{2\pi}\sigma_0}\text{ exp}\left( -\frac{\lVert w\rVert^2}{2\sigma_0^2} \right)$$

目标是求$w$的最大后验估计MAP, 也就是$\hat{w} = \text{ argmax}_w \ P(w|y)$。由bayes公式得：

$$P(w|y) = \frac{P(y|w)P(w)}{P(y)}$$

因为$y$是由数据集给定的，可以看做常量，再加入对数操作简化计算，可以简化成：

$$\text{ argmax}_w \ P(w|y)= \log P(y|w)P(w)$$

即：

$$\begin{align} \text{ argmax}_w \ P(w|y) = & \sum_{i=1}^{N}\log \frac{1}{\sqrt{2\pi}\sigma}\text{ exp}\left( -\frac{(y_i - w^Tx_i)^2}{2\sigma^2} \right) \frac{1}{\sqrt{2\pi}\sigma_0}\text{ exp}\left( -\frac{||w||^2}{2\sigma_0^2} \right) \\ = & \sum_{i=1}^{N}\log \frac{1}{2\pi\sigma\sigma_0}\text{ exp}\left( -\frac{(y_i - w^Tx_i)^2}{2\sigma^2} -\frac{||w||^2}{2\sigma_0^2} \right) \\ = & \sum_{i=1}^{N} \log \frac{1}{2\pi\sigma\sigma_0} + \log \text{ exp}\left( -\frac{(y_i - w^Tx_i)^2}{2\sigma^2} -\frac{||w||^2}{2\sigma_0^2} \right) \end{align}$$

因为$\log \frac{1}{2\pi\sigma\sigma_0}$与 最大化$P(w|y)$无关，可以舍去，即：

$$\begin{align} \text{ argmax}_w \ P(w|y) = & \sum_{i=1}^{N} \log \text{ exp}\left( -\frac{(y_i - w^Tx_i)^2}{2\sigma^2} -\frac{||w||^2}{2\sigma_0^2} \right) \\ = & \sum_{i=1}^{N} -\frac{(y_i - w^Tx_i)^2}{2\sigma^2} -\frac{||w||^2}{2\sigma_0^2} \\ \end{align}$$

进一步简化的：

$$\begin{equation} \text{ argmax}_w P(w|y) = \sum_{i=1}^{N} (y_i - w^Tx_i)^2 + \frac{\sigma^2}{\sigma_0^2}||w||^2 \end{equation}$$

这样跟从频率角度得到的岭回归结果一样。即最小二乘估计中隐藏一个假设：噪声服从高斯分布。即正则化的最小二乘法等价于最大后验估计MAP，其中噪声为高斯分布，并且假定$w$也服从高斯分布。