Lecture 11 PageRank and Ridge Regression
Lecture 11: PageRank and Ridge Regression
1. PageRank
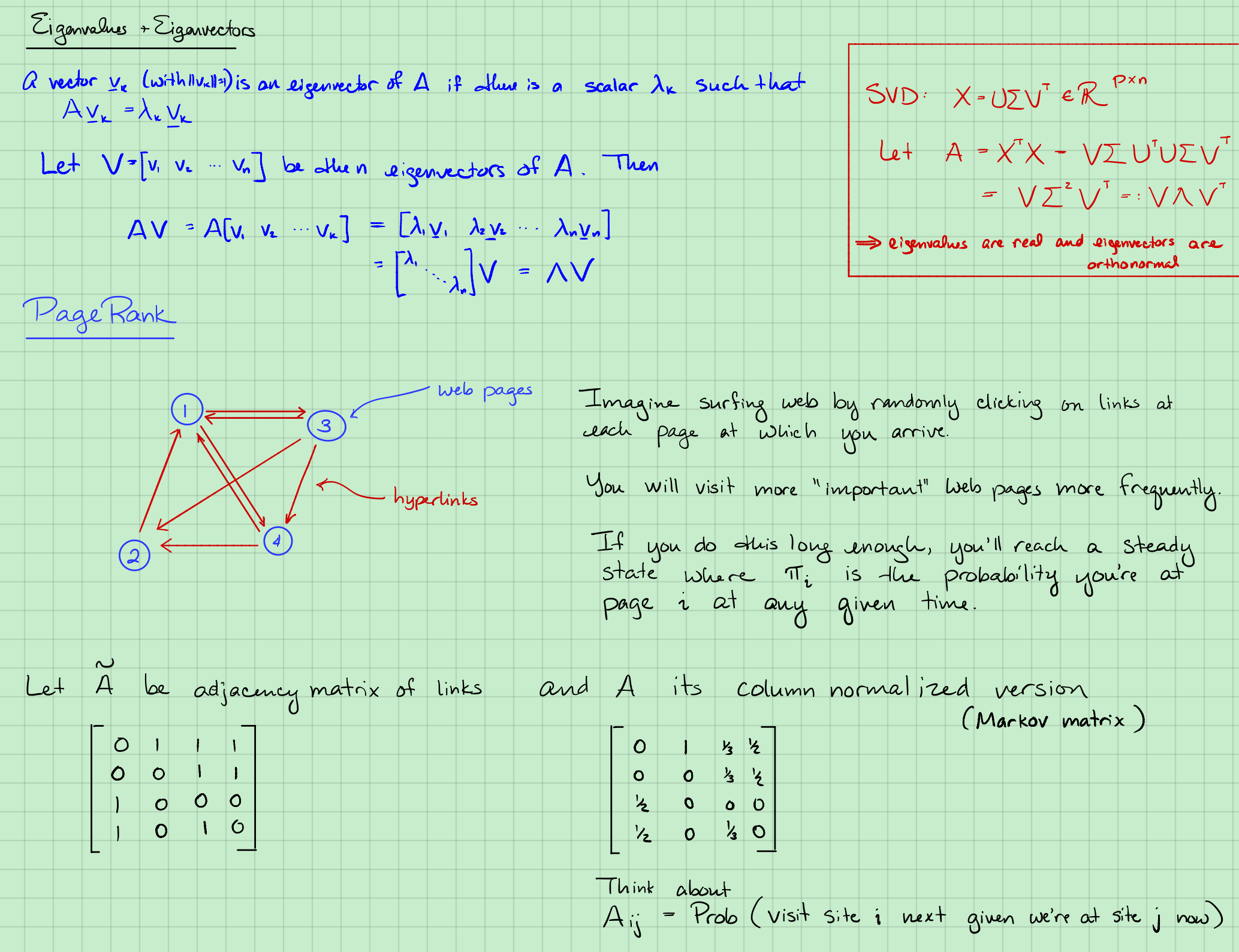

Google PageRank
- Imagine surfing web by randomly clicking links. This is called a “random walk” over graph. If you do this long enough eventually reach “steady state” where Probability that you are at site
让$\tilde A$ 表示这个图的邻近矩阵,其中:
具体地有:
接下来,让$A = \tilde A $ column-normalized version.
定义:$e_{i} = i^{th}$单位矩阵$I$的第$i$列。
那么,
$A_ij= Pro(\text{go to site i }| \text{ at site j})$.我们从$j$到$i$的可能性。
令:
$\underline{\pi} $是到下一个网站的可能性,而且有:
目标是找到 。
令 是的特征向量。
对于:
$X$的$\sigma$的平方就是$A$的特征值。$X$右奇异向量就是$A$的特征向量。
PageRank 矩阵$A$有$\lambda_1=1 > \lambda_2 \ge\lambda_3 \ge \cdots\ge \lambda_n$.

算法流程
又有:
和
接下来证明算法为什么会有效?
假定特征向量是orthonormal($V^TV=VV^T=I$)。
相应地:
其中,$v_1就等于\underline{\Pi}$.那么,
而
那么式10等于:
当$k \to \infty$,$\frac{\lambda^k_i}{\lambda_1^k} \to 0 \ for \ i \ne 1$,那么
那么式12等于
Classical Ridge Regression


本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 aigonna!
评论






