Lecture 10 More on the SVD in Machine Learning

Lecture 10: More on the SVD in Machine Learning including matrix completion

1. SVD in machine learning

Dimensionality Reduction(PCA)
Principal Components Regression
Least Squares
Matrix Completion
PageRank

2. Least Squares & SVD

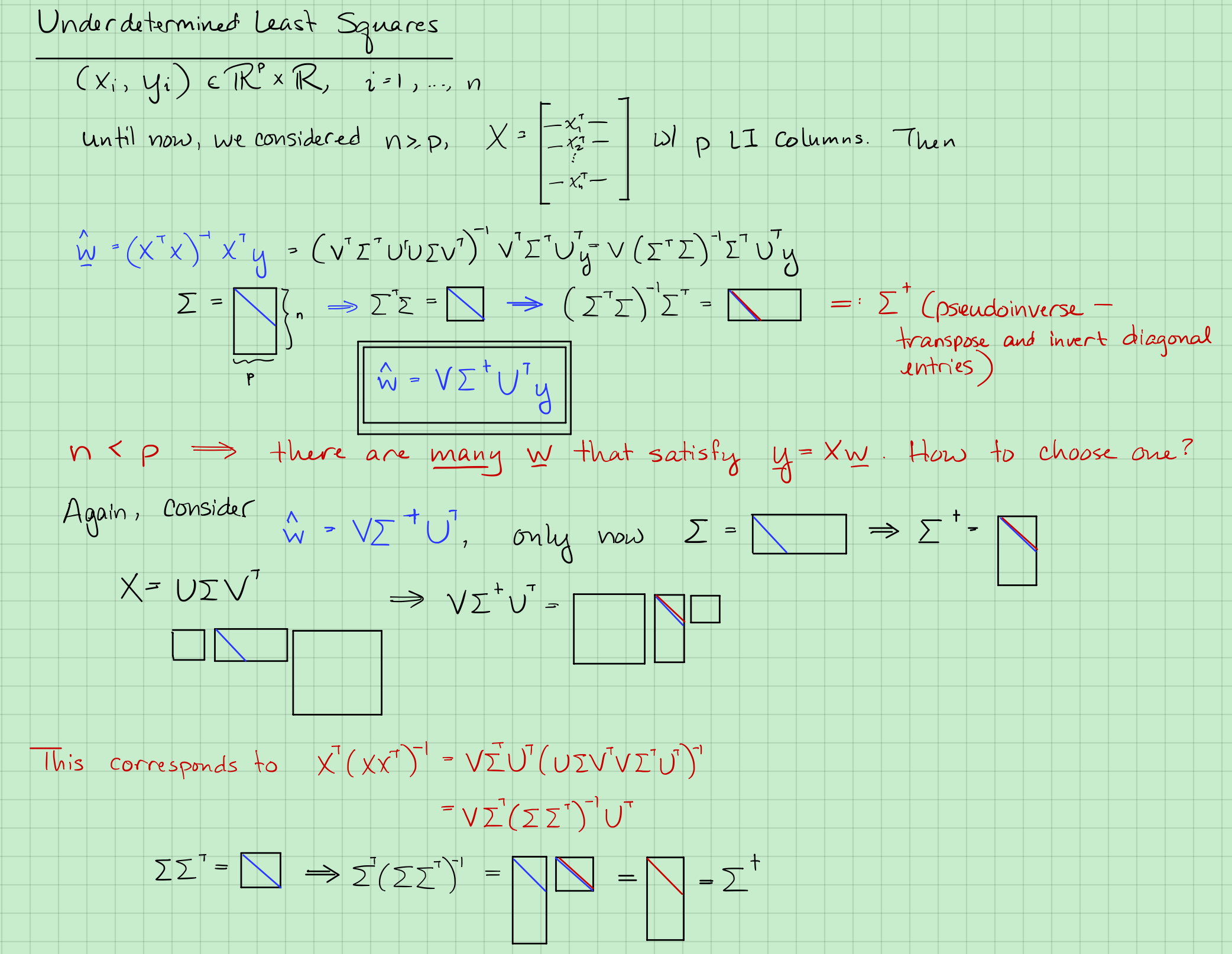
理解最小二乘

理解最小二乘续

跟前面提到的一样有：

假设$n \ge p$ & $X$有$p$个线性无关的列，那么

$\hat w = (X^TX)^{-1}X^Ty \tag{1}$

情形1：

如果$X= U \Sigma V^T$,其中$U : n\times n ,\ \ \Sigma: n \times p ,\ \ V^T: p \times p$, 那么

$(X^TX)^{-1}X^T = (V \Sigma^T U^T U \Sigma V^T)^{-1}V\Sigma^TU^T=(V \Sigma^T \Sigma V^T)^{-1}V\Sigma^TU^T\tag{2}$

由下面两式,

$VV^T = V^TV= I \Rightarrow V^{-1}=V^T \\ (AB)^{-1}=B^{-1}A^{-1}$

可得:

$(AV^T)^{-1} = (V^T)^{-1}A^{-1}=VA^{-1}\tag{3}$ $(VB)^{-1}=B^{-1}V^{T} \tag{4}$ $(VAV^T)^{-1}= VA^{-1}V^T \tag{5}$

继续化简式2，[利用式5，把 $\Sigma^T \Sigma$ 看作 $A$ ]

$(X^TX)^{-1}X^T = V(\Sigma^T \Sigma)^{-1}V^TV\Sigma^TU^T=V(\Sigma^T \Sigma)^{-1}\Sigma^TU^T\tag{6}$

pseudo-inverse:

$\Sigma^+ = (\Sigma^T \Sigma)^{-1}\Sigma^T \tag{7}$

并且有上节课里提到的：

$\underbrace{ (\Sigma^T \Sigma)^{-1}\Sigma^T}_{p \times n}=\left[\begin{array}{cccc|c} 1/\sigma^{2}_1 & 0 & \cdots & 0 &\\ 0 & 1/\sigma^{2}_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1/\sigma^{2}_p \end{array} \right]=\Sigma^+$

由式7得：

$(X^TX)^{-1}X^T =V\Sigma^+U^T\tag{8}$

跟上节课一样：

$\hat w \approx V\Sigma^+U^Ty\tag{9}$

情形2：

$p \ge n$, $X$ 有$n$个独立的行，

那么有无数解[ 无穷个 $w$ 满足 $\hat y = Xw$ ].

Claim: $\hat w = V \Sigma^+ U^T$ has the smallest norm of any w $s.t: \ y = Xw$。我们从上面的$w$中挑出一个$\hat w$来使其有最小的范数，并且满足约束。

$V\Sigma^+U^T = X^T (X^TX)^{-1}\tag{10}$

因为$X$是“瘦长型”矩阵，那么其伪逆为$\Sigma^+= \Sigma^T(\Sigma\Sigma^T)^{-1}$。

对于任意$w$要有$y = Xw$.我们想要得到

$\lVert w \rVert^2_{2} \ge \lVert \hat w \rVert^2_{2}$

而，

$\lVert w \rVert^2_{2} = \lVert w - \hat w + \hat w \rVert^2_{2}\tag{11}$

回忆一下，

$\lVert a +b \rVert^2_{2} = (a+b)^T(a+b)=a^Ta-2a^Tb+b^Tb=\lVert a\rVert^2_{2}-2a^Tb+\lVert b \rVert^2_{2}\tag{12}$

式11,变为：

$\lVert w - \hat w + \hat w \rVert^2_{2} = \lVert w - \hat w \rVert^2_{2} -2(w-\hat w)^T\hat w + \lVert \hat w \rVert^2_{2} \tag{13}$

我们现在只看中间项，它等价于, 利用 $\hat w=X^T(XX^T)^{-1}y$ 跟伪逆一样理由写成这样化简下：

$(w-\hat w)^T\hat w =(w-\hat w)^TX^T(XX^T)^{-1}y=\underbrace{(X(w-\hat w))^{T}}(XX^T)^{-1}y\tag{14}$

又因为 $y = X w = X\hat w \Rightarrow X\hat w -Xw =X(w-\hat w) =\boldsymbol{0}$ 。只能是 $(w-\hat w) =\boldsymbol{0}$ .

所以式12等于：

$\begin{aligned} \lVert w - \hat w + \hat w \rVert^2_{2} &= \lVert w - \hat w \rVert^2_{2} +\lVert \hat w \rVert^2_{2} \\ &\Rightarrow \lVert w \rVert^2_{2} \ge \underbrace{\lVert w - \hat w \rVert^2_{2}}_{\ge 0} +\lVert \hat w \rVert^2_{2} \\ &\Rightarrow \lVert w \rVert^2_{2} \ge \lVert \hat w \rVert^2_{2} \end{aligned} \tag{15}$