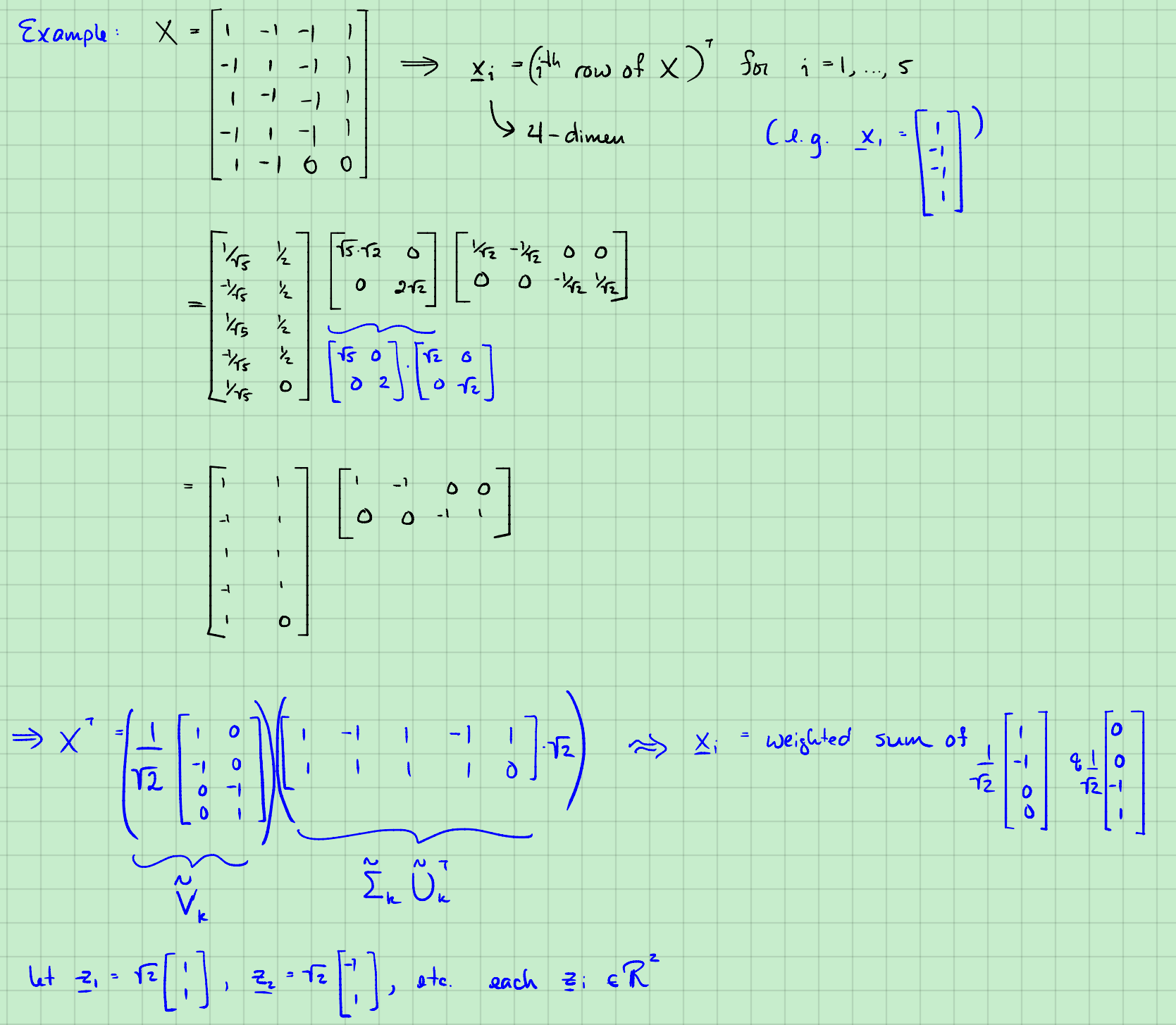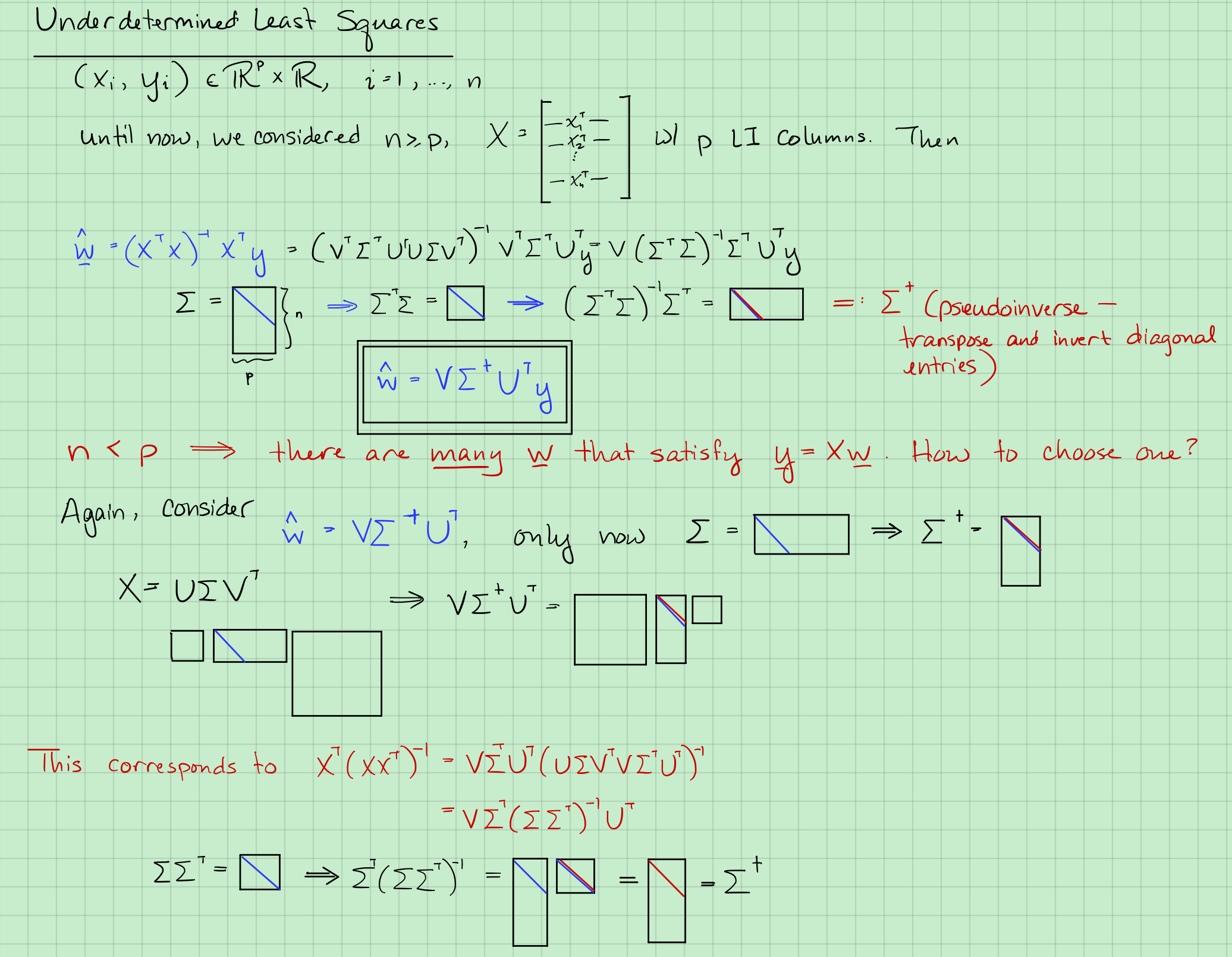Lecture 9 The SVD in Machine Learning

矩阵表示
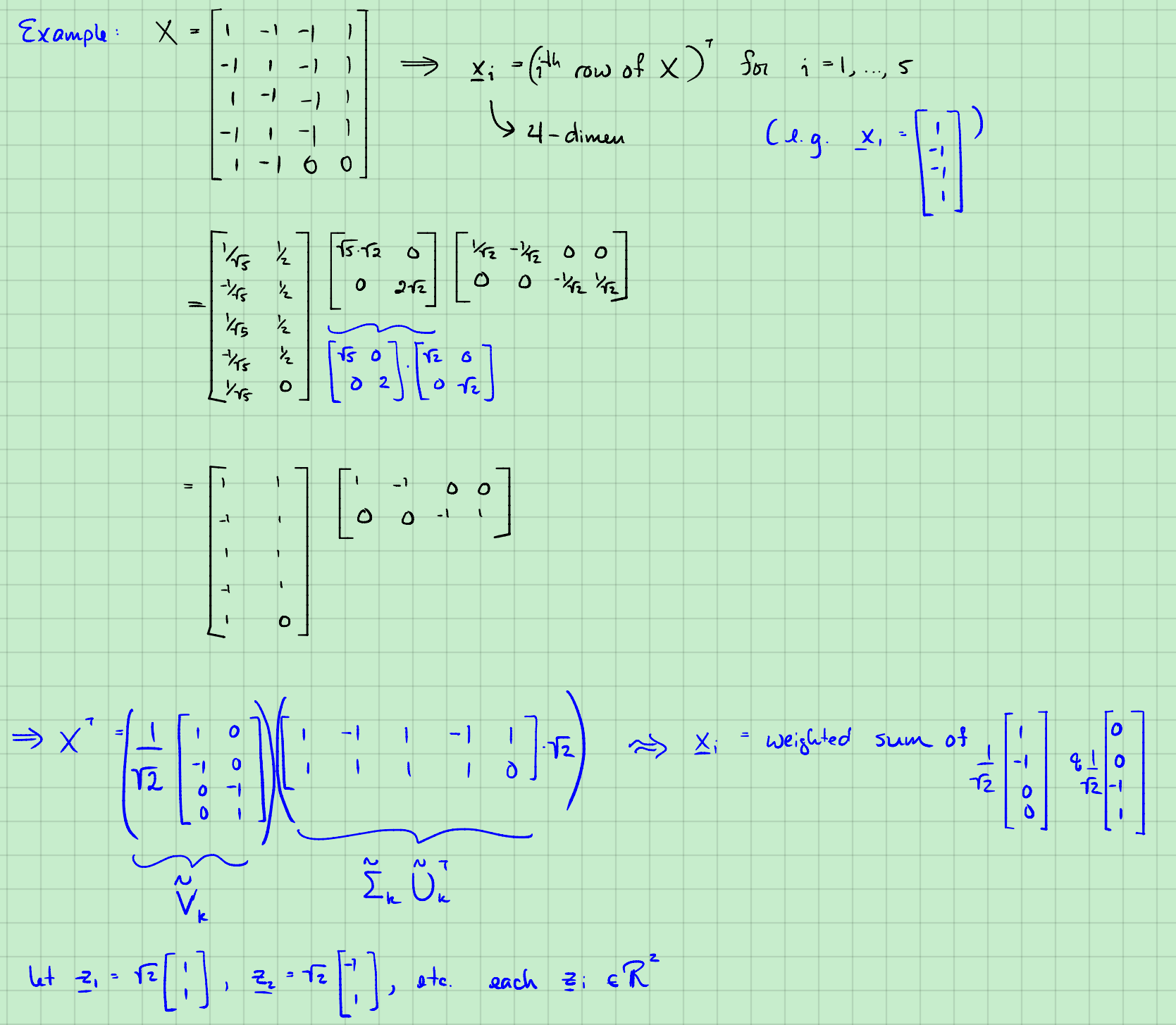
其实是利用从列向量乘法来分解的,$X$第一列是由:
这不是SVD,不是奇异值。
$X$的秩是2,列向量、行向量最大为2.
上面接下来才是SVD。
Python numpy SVD结果如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| import numpy as np
A = np.mat([[1, -1, -1, 1],
[-1, 1, -1, 1],
[1, -1, -1, 1],
[-1, 1, -1, 1],
[1, -1, 0, 0]])
u, s, vt = np.linalg.svd(A)
print("U:", u,'\n', "Sigma:", s, '\n', "VT:",vt)
OUT:
U: [[-4.47213595e-01 -5.00000000e-01 7.11769812e-01 2.08287624e-01
1.00420616e-17]
[ 4.47213595e-01 -5.00000000e-01 -3.37852315e-02 -1.24600260e-01
7.30296743e-01]
[-4.47213595e-01 -5.00000000e-01 -7.00888060e-01 2.34632102e-01
-6.08580619e-02]
[ 4.47213595e-01 -5.00000000e-01 2.29034795e-02 -3.18319466e-01
-6.69438681e-01]
[-4.47213595e-01 -5.55111512e-17 -2.17635041e-02 -8.85839452e-01
1.21716124e-01]]
Sigma: [3.16227766e+00 2.82842712e+00 2.95877601e-16 4.03361097e-17]
VT: [[-7.07106781e-01 7.07106781e-01 0.00000000e+00 0.00000000e+00]
[-7.02166694e-17 -7.02166694e-17 7.07106781e-01 -7.07106781e-01]
[ 2.98602000e-01 2.98602000e-01 -6.40965557e-01 -6.40965557e-01]
[ 6.40965557e-01 6.40965557e-01 2.98602000e-01 2.98602000e-01]]
|
$X^T=\tilde V \tilde \Sigma \tilde U^T $
最小二乘的SVD
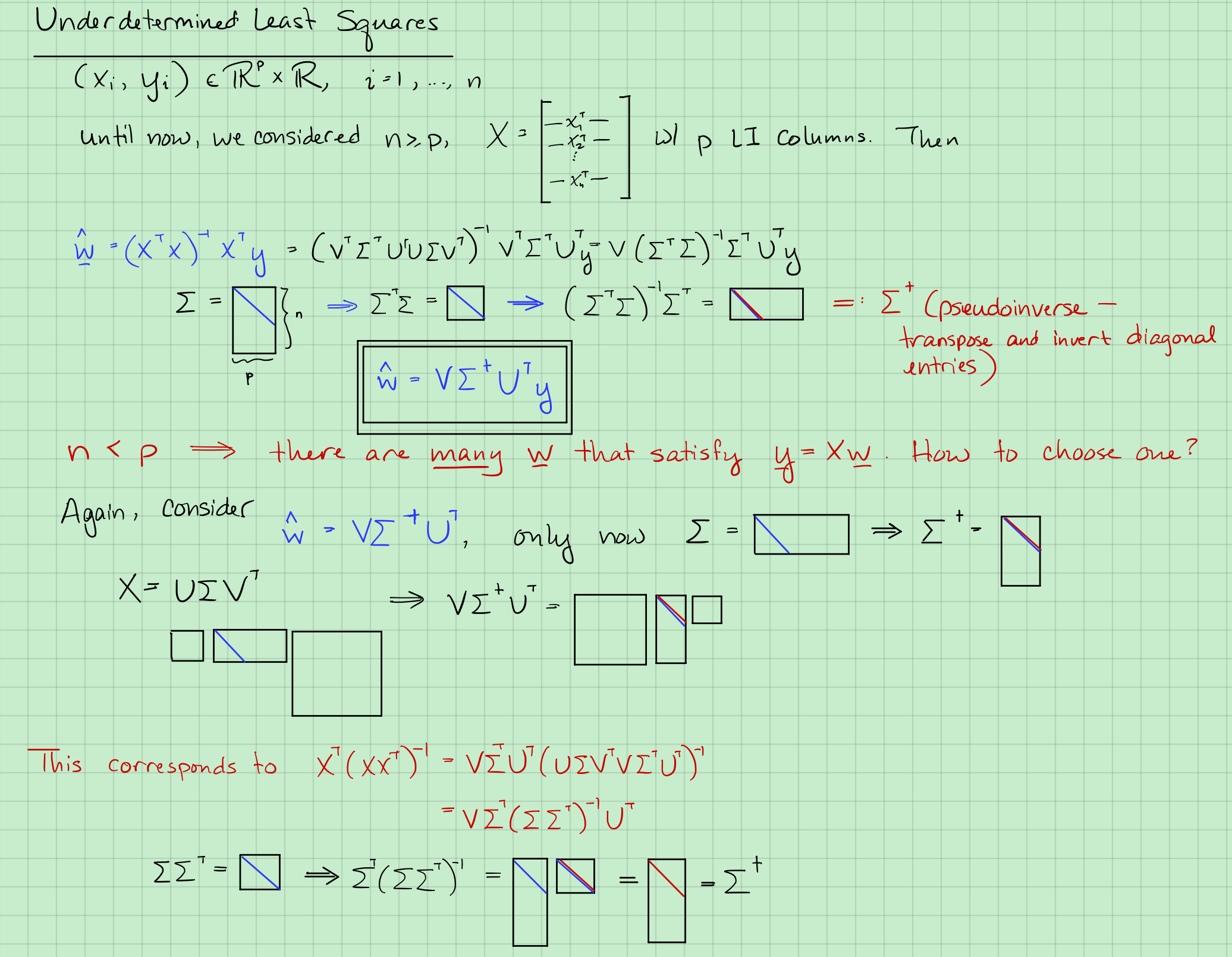
对于均是方阵$(AB)=B^{-1}A^{-1}$。另外$U^TU=U^TU=I=UU^{-1}$。
式2变为:
$V^TV=VV^T=I=VV^{-1} \Rightarrow V^T=V^{-1}$
因为$n \ge p$,$\Sigma$矩阵是瘦长型,下面全是0.$\Sigma$是$n \times p$,那么$\Sigma^T\Sigma$是$p \times p$。即
那么,竖线后面全是0
又叫做$\Sigma$的pseudo-inverse。
$ w$估计为:
证明: