Lecture 8 The Singular Value Decomposition
Lecture 8 The Singular Value Decomposition
1. SVD
$X \in \mathbb{R}^{n \times p}$有SVD $U\Sigma V^T$,并且满足:
- $U \in \mathbb{R}^{n \times n}$是正交的$UU^T=U^TU=I$ [ $U$的列=左边奇异向量]
- $V \in \mathbb{R}^{p \times p}$是正交的$VVT=V^TV=I$ [ $V$的列=右边奇异向量]
- $\Sigma \in \mathbb{R}^{n \times p}$是对角阵,并且对角元素满足$\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_p$。
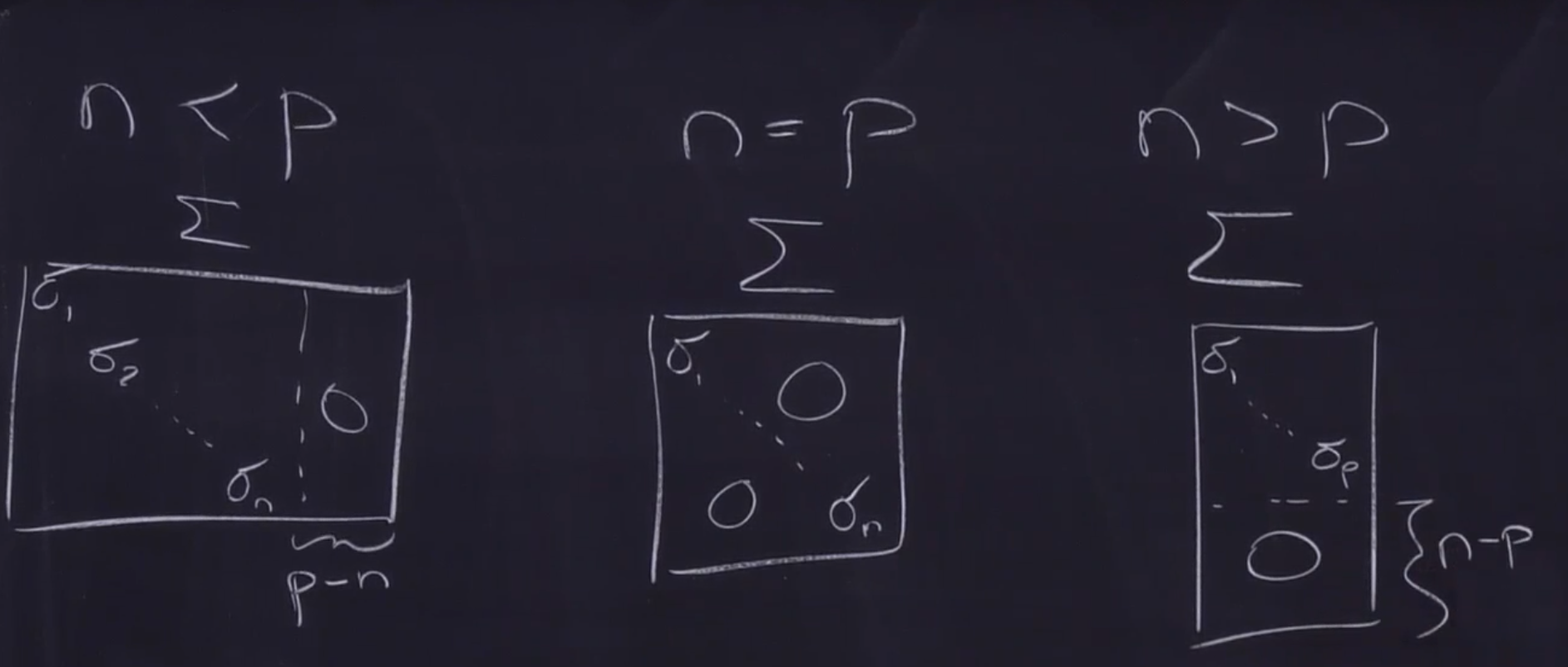
SVD示意图
1 | import numpy as np |
注意上面,SVD 中$U, \Sigma, V$变化
对于上面第三个例子,$SVD(X)=(U\Sigma V^T)^T=V\Sigma U^T$
奇异值会按照从大到小排,这跟最小化投影有关。

奇异值变化
等价地,我们可以用rank-1的矩阵的和表示矩阵$X$
其中,$U_i$是$U$的第$i$列,$V_i^T$是$V$的第$i$列。

2. The subspace approximation Theorem
给定$X \in \mathbb{R}^{n \times p}$,$rank (X) = r \le min(p, n)$。矩阵的秩等于奇异值大于0的个数$num(\sigma_i \ge 0)$。
找一个$X_k \in \mathbb{R}^{n \times p}$,并且$rank (X_k) = k < r$,作为尽可能接近$X$。(as “close “ as possible to X).
Frobenius norm :
近似矩阵$\tilde X$的SVD有:
- $\tilde \Sigma \in \mathbb{R}^{r \times r}对角元素 \tilde \sigma_1 \ge \tilde \sigma_2 \ge \dots \ge \tilde \sigma_p.$
- $\tilde U \in \mathbb{R}^{n \times r}, \tilde U^T\tilde U=I, but \ \tilde U\tilde U^T \ne I $
- $\tilde V \in \mathbb{R}^{p \times r}, \tilde V^{T}\tilde V=I, but \ \tilde V\tilde V^T \ne I $

Singular Value Spectrum:
3. The “ Economy SVD”

4. 降维

给定$X_i \in \mathbb{R}^p \ for \ i=1, \cdots, n$,找到对于$k < p \ for \ i=1, \dots, n 的Z_i \in \mathbb{R}^k $,有跟$X_i$同样的性质。
其中,
- $V_k$: $p \times k$ 对于最好的k-dim子空间的基。
- ${\Sigma}U^T_k$ 第i列是对$\tilde X_i$k组基的系数。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 aigonna!
评论






