Lecture 7 Introduction to the Singular Value Decomposition

Lecture 7 Introduction to the Singular Value Decomposition

1. 问题引入和投影矩阵的性质

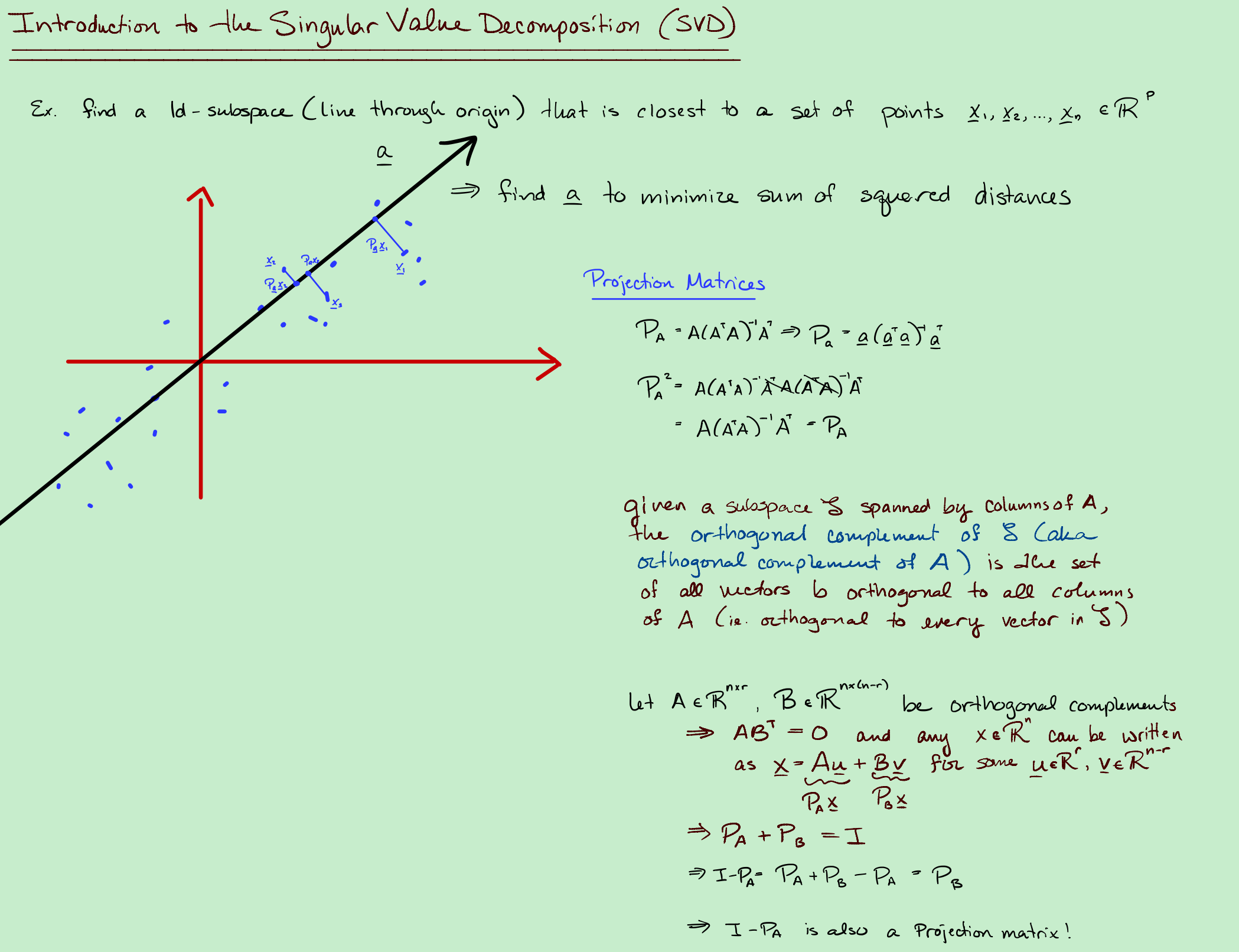
Goal:对于观测值$X_1, X_2,\cdots, X_p \in \mathbb{R}^n$,找到一个一维子空间(可以理解为一根直线)能”最好的拟合数据”

Solution：

$$\text{ 把每一个 }X_i \text{ 投影到 } \overrightarrow a上， Proj^{X_i}_{\overrightarrow a} \ , \text{ 投影到让距离 } d^2_i=\lVert X_i- Proj^{X_i}_{\overrightarrow a}\rVert^2_{2} 和最小。$$

复习Projection Matrices：

If $A \in \mathbb{R}^{n \times p}$张成的子空间，那么Projection of $X$ onto $span(cols(A))=Proj_A X$，如果$A$的每列都是线性无关的，并且有：

$$Proj_A X = A(A^TA)^{-1}X \tag{1}$$

其中，$P_A=A(A^TA)^{-1}A^T$。

还有性质：

1. $$P_A = P^{2}_A=P_AP_A=P^T_{A}=P^T_{A}P_A \tag{2}$$

2. If $A = \boldsymbol{a}$,

   $$P_{\boldsymbol{a}} = \boldsymbol{a}(\boldsymbol{a}^T\boldsymbol{a})^{-1}\boldsymbol{a}^T=\frac{\boldsymbol{a}\boldsymbol{a}^T}{\boldsymbol{a}^T\boldsymbol{a}}\tag{3}$$

   因为$(\boldsymbol{a}^T\boldsymbol{a})^{-1}$是一个标量(可以看详细投影矩阵的证明)。

1. The orthofonal complement of a subspace is the set of all vectors orthogonal to the subspace.

   子空间的正交补 orthofonal complement 是所有正交于子空间的向量的集合(这个子空间是正交子空间)。并且：$A^TB=0$（正交）

   (不是这个图的示意，是)如果$A \in \mathbb{R}^{n \times r0}$,那么$B \in \mathbb{R}^{n \times (n-r)}$。维度上和不变，正交补的维度是其差。

对于任意的$X \in \mathbb{R}^n$,能写作：

$$IX = P_AX+P_BX =(P_A + P_B)X \Rightarrow I=P_A+P_B \ \Rightarrow P_B=I-P_A\tag{4}$$

正交空间

2. 证明最小距离和、引入奇异向量奇异值

将$P_a$用式3代入，然后相当于做了提取公因子$X_i$ [拓展作单位矩阵 $IX_i$ ]，那么$I-\frac{aa^T}{a^Ta}$可以看作投影矩阵$I-P_a$,由式4可得这也是投影矩阵$P_B$,这就是正交补。再写作内积展开式，由性质2公式3可以知道$(I-\frac{aa^T}{a^Ta})^T(I-\frac{aa^T}{a^Ta})=I-\frac{aa^T}{a^Ta}$.

​ 而$X_i^TX$是常数跟$a$无关。即只要最大化$\frac{X_iaa^TX_i}{a^Ta}$.

​ $a^TX_i$是标量。

​

$$\begin{aligned} XX^T&= \left[\begin{array}{ll} | & |&|&|\\ X_{1} & X_{2}&\cdots&X_{p} \\ | &| &|&| \end{array}\right] \left[\begin{array}{ll} - & X_{1}^{\top}&- \\ - & X_{2}^{\top}&- \\ - & \vdots &- \\ - & X_{p}^{\top}&- \end{array}\right] \\ &=X_1X_1^T+X_2X_2^T+\cdots+X_pX_p^T\\ &=\sum^{p}_{1}X_iX_i^T \end{aligned}\tag{5}$$

​ 用式5矩阵的外积，写作矩阵外积去掉求和，只要求$argmax_{a}(\frac{a^TXX^Ta}{a^Ta})$。

现在定义一些名词：

1. 使得上是取得最大值的向量$\hat{\boldsymbol{a}}$称作$\boldsymbol{X}$的第一个左奇异向量。

2. $\frac{a^TXX^Ta}{a^Ta}=\sigma^{2}_1$(这里没用黑粗体懒得写了)的值称作$X$第一个奇异值。

   $$\begin{aligned} \frac{a^TXX^Ta}{a^Ta}&=\sigma^{2}_1\\ &= \lVert X \rVert^2_{op} \ \text{"operator norm"}\\ &=\lVert X \rVert^2_{2} (跟向量2范数有别) \end{aligned}\tag{6}$$

3. 奇异值分解

$U$的列向量是$X$的列向量的正交基。

$\Sigma$是没有负元素的对角矩阵，$\sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_p$。

令$U = [U_1, U_2, \cdots, U_n]$, $U_1$is the best 1d subspace fit to $X_i’$s。也是上面式6的解。

令 $\tilde X_i^{(1)} = X_i - Proj_{U_1}{X_i}$ ，

​

$$U_2= \text{ the best 1d subspace fit to } \tilde X_i' s.$$

若$X_{n \times p} $有秩$r < min(n, p)$。

thin $\Sigma$。

4. PCA