Lecture 5 Subspaces, Bases, and Projections
Lecture 5 Subspaces, Bases, and Projections
1.回想最小二乘的几何意义引入span
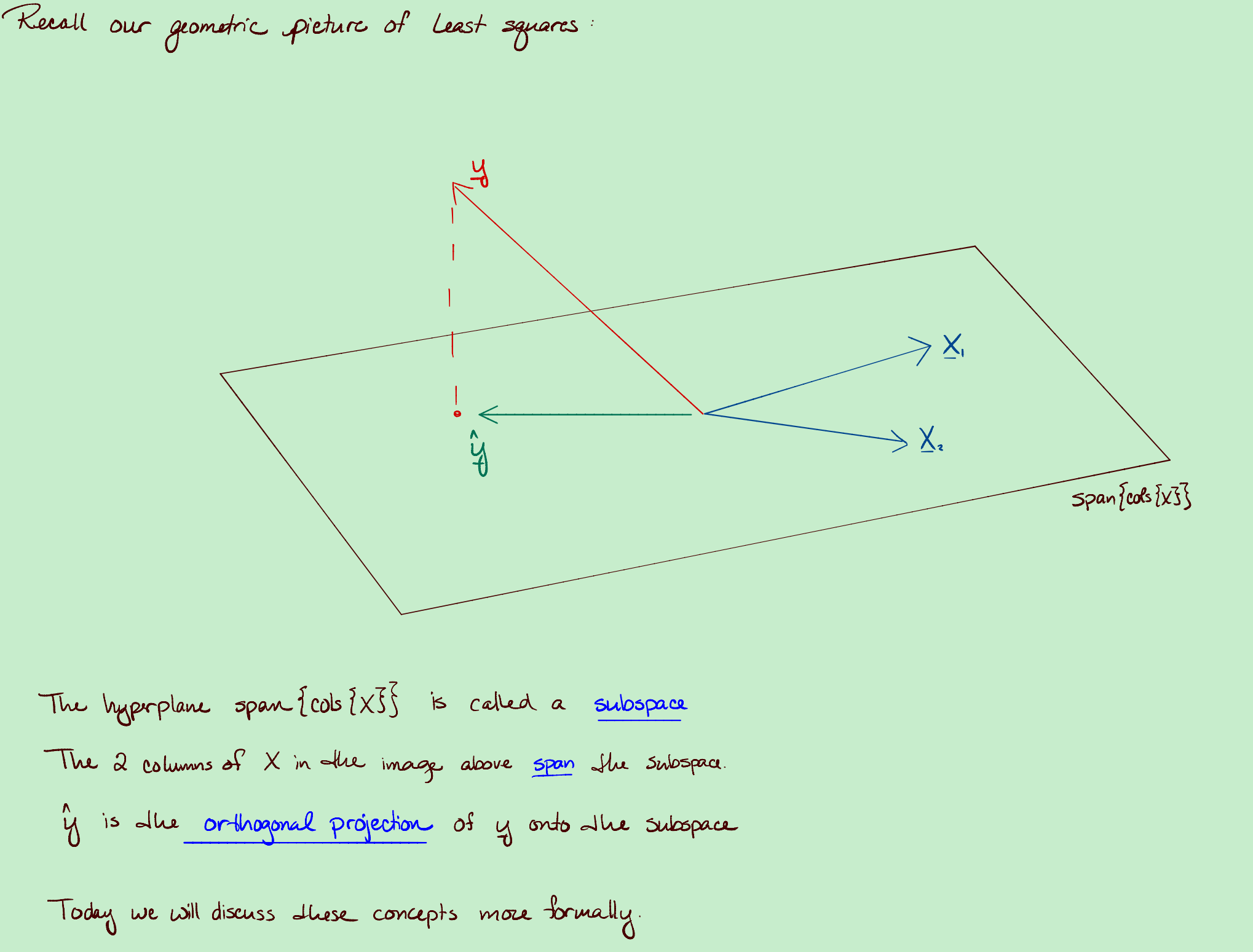
上面的平面可有$X$的列向量的张成空间$X$。
2. subspace
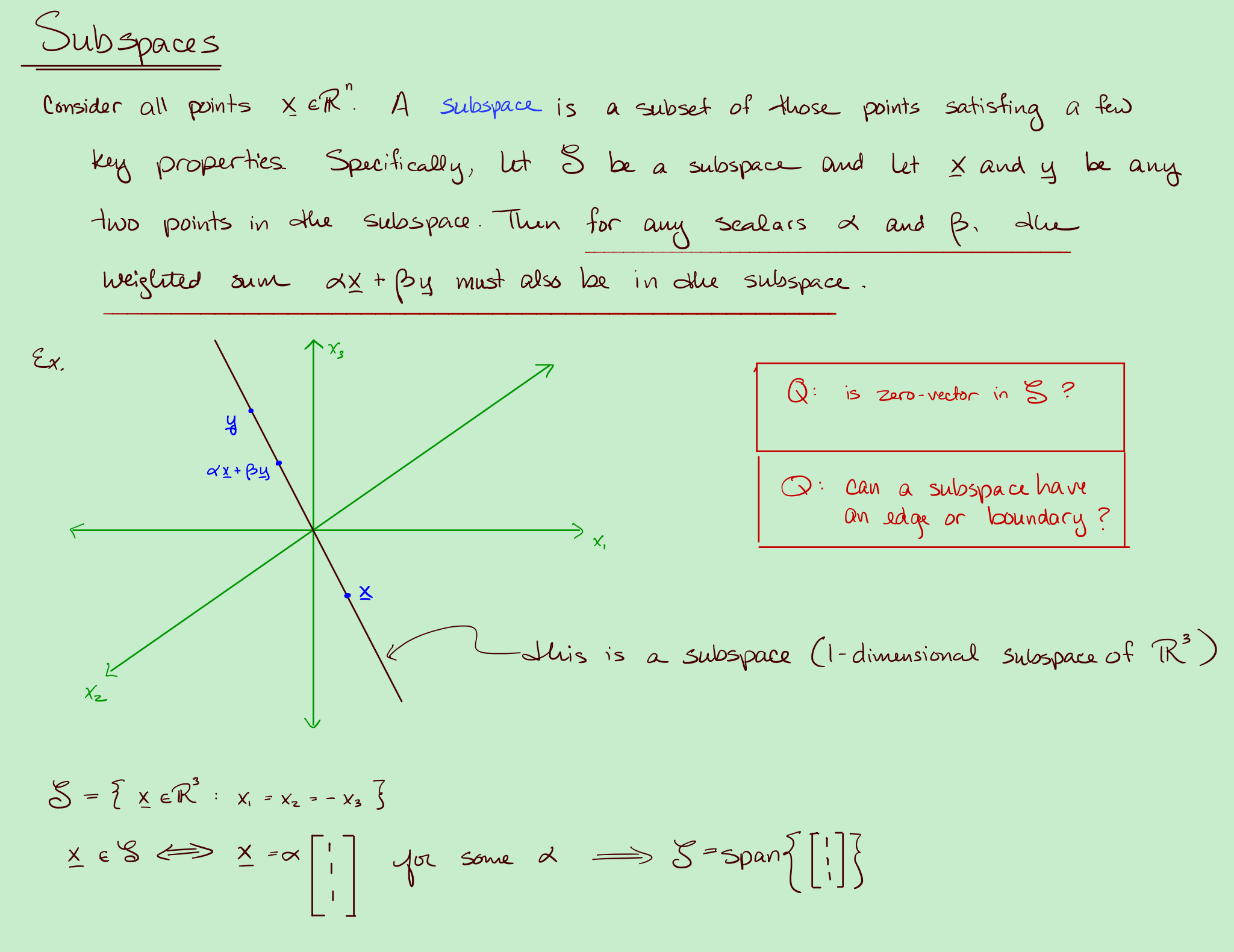
If the cols of $X$ are Linearly Independent, $X$ is a subspace. Then they form a basis for $X$.
上上图中的(绿色点)$\hat {\underline y}$是$\underline{y}$在$X$上的投影。
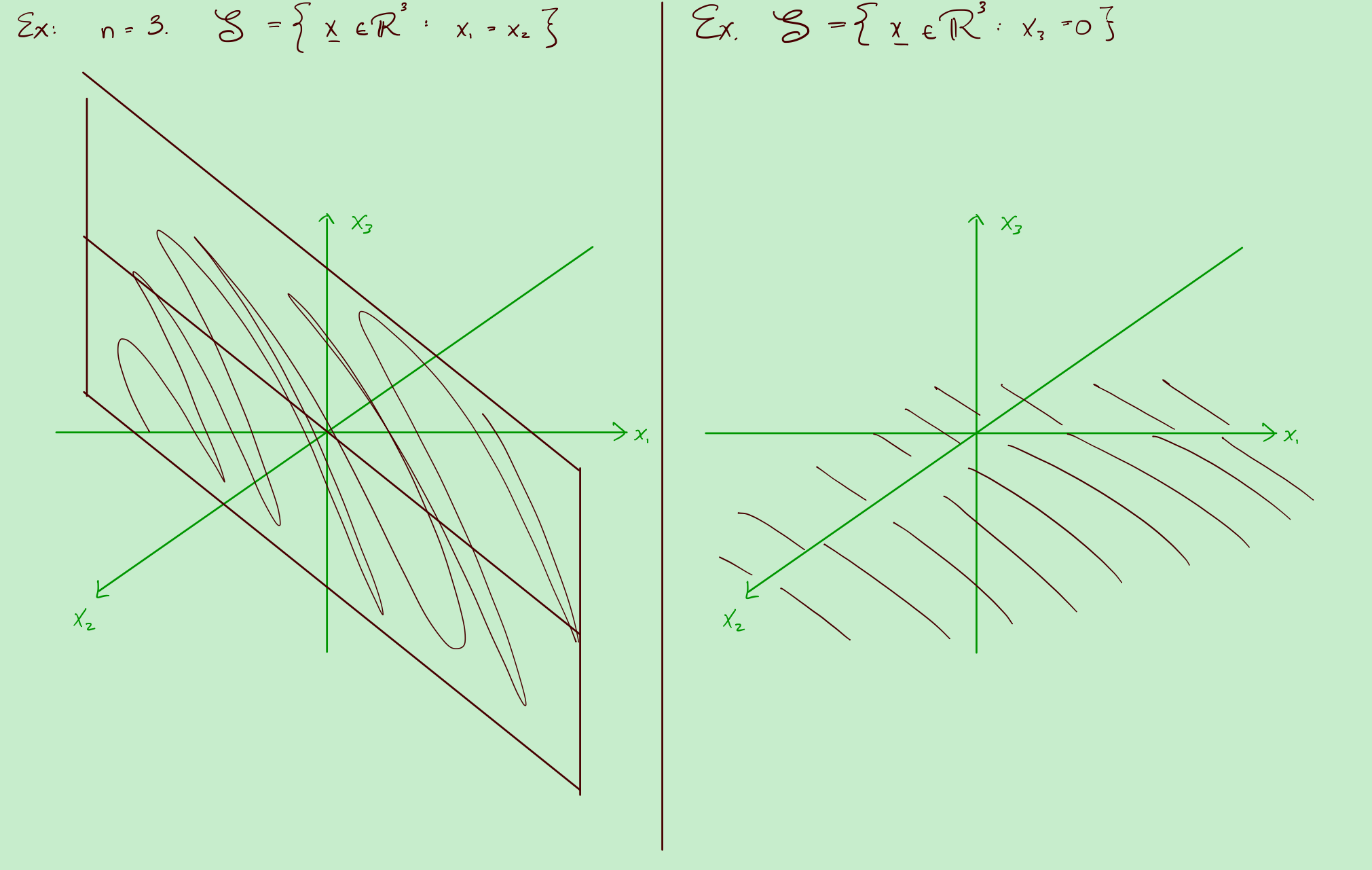
vertical plane
horizontal plane
子空间永远包含原点或者说$\overrightarrow{0}$。
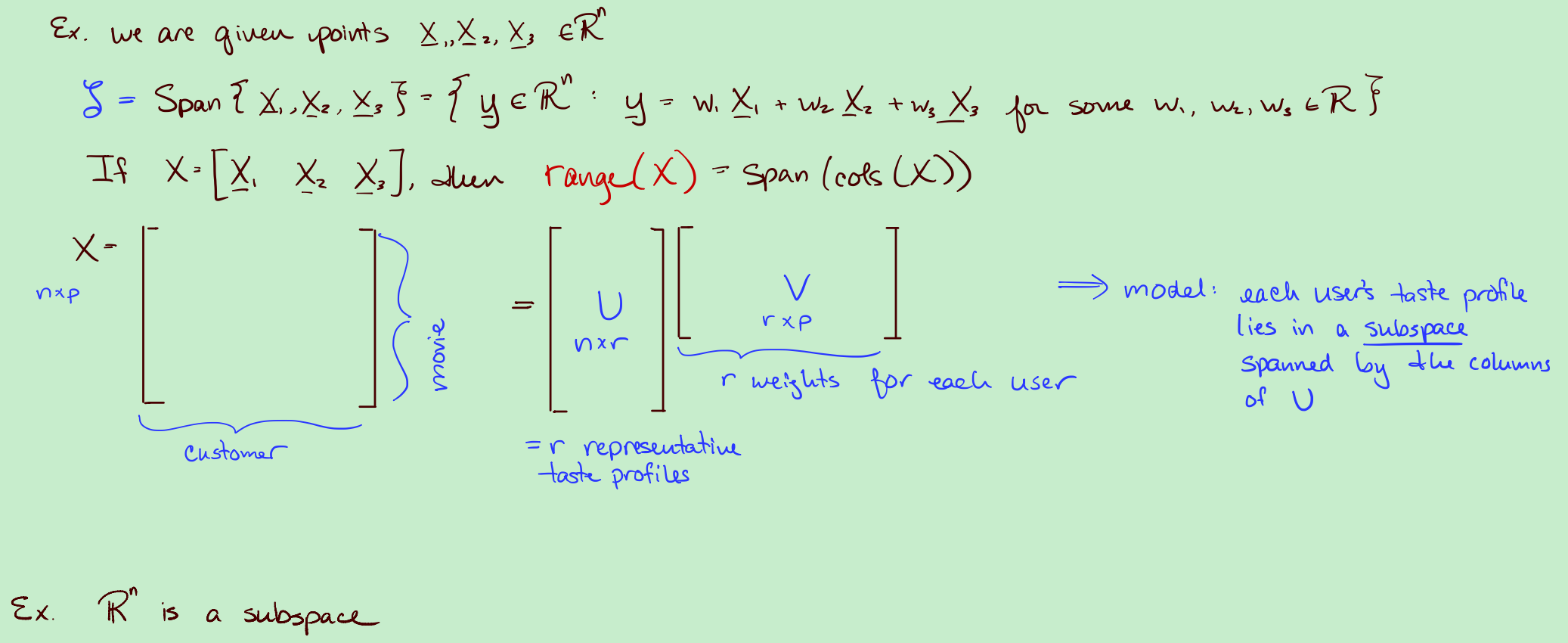
3. 怎么表示一个子空间?

- 用一组向量的集合作为一个张成子空间
- 用一组线性无关的向量张成子空间,这组向量叫一组基
- 用一组正交单位向量(orthonormal vector)张成子空间,这组向量又叫正交单位化基,正交基。
orthonormal:
- ortho : orthogonal
- normal: norm(length=1)
理解正交、单位向量
那么,两个向量$u_1$和$u_2$都是正交的。
那么$u$是单位化的。
这组向量$u_1, u_2, \cdots, u_p$是正交单位向量
4. 正交矩阵及其性质

The matrix $U$ is orthogonal in this setting if it is a $p \times p$ square matrix. If it’s an $n \times p$ matrix with $n>p$, then $U $gives a basis for a subspace but it is not an orthogonal matrix. In this case, $U^TU=I$, but $UU^T$ is not = $I$.
如果$u_1, \cdots, u_p$是正交单位化的,且$\delta = span (u_1, \cdots, u_p)$,那么
性质1:
性质2:
记个记号:dimension of subspace , $dim(\delta)$=子空间基向量的个数。
如果一个子空间有矩阵$X$的列向量张成,那么$dim(\delta)=rank(X)$。
5. 矩阵中含有线性无关(列或行)向量的数目?

$X \in \mathbb{R}^{n\times p}$,$r=rank(X)\leq min(n,p)$ , 假设$n \geq p \Rightarrow r \leq p$。
我们能在$\mathbb{R}^n$上有多于n个线性无关的向量?——不能。
6. Projection
一个点的投影到一个集上是这个集上离这个点最近的点。


$(X^TX)^{-1}X^T$又叫作投影矩阵, 记作$P_X$。
用投影的定义来最优化解决问题。
$P_X$的性质:
- 方阵
- $P_X=P_XP_X=P^2_X$
从定义很容易证明,投影的投影就是本身。
7. 正交基子空间和最小二乘法
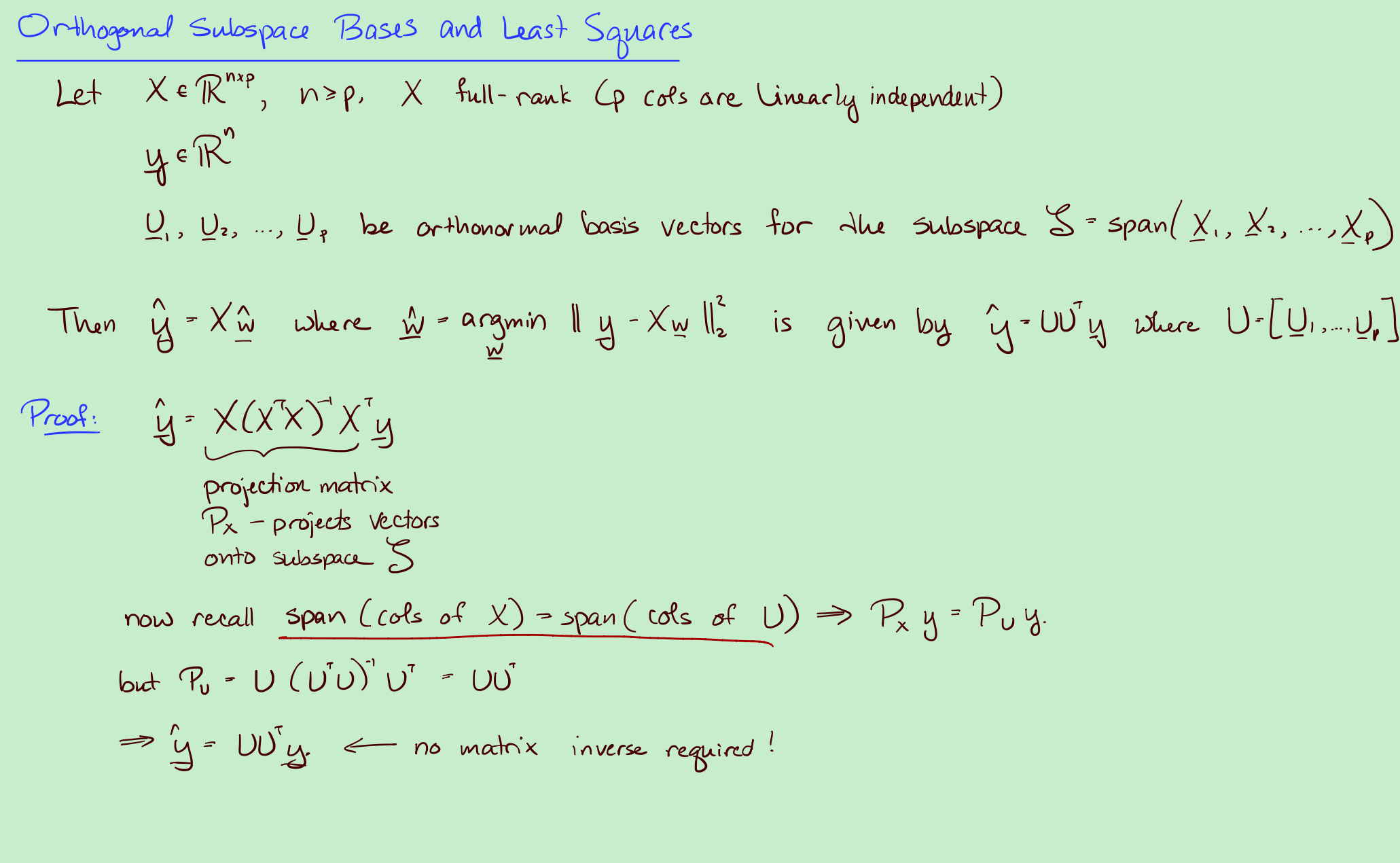
这里用全新的角度来解决上述中非常难计算的$P_X=(X^TX)^{-1}X^T$。
找到一组正交基向量使得$span(X_1, X_2, \cdots, X_p)=span(U_1, U_2, \cdots, U_p)$即$span(cols(U))=span(cols(X))$。
那么$P_Xy=P_Uy$,就有$\hat y = UU^Ty$。不要矩阵的逆了。
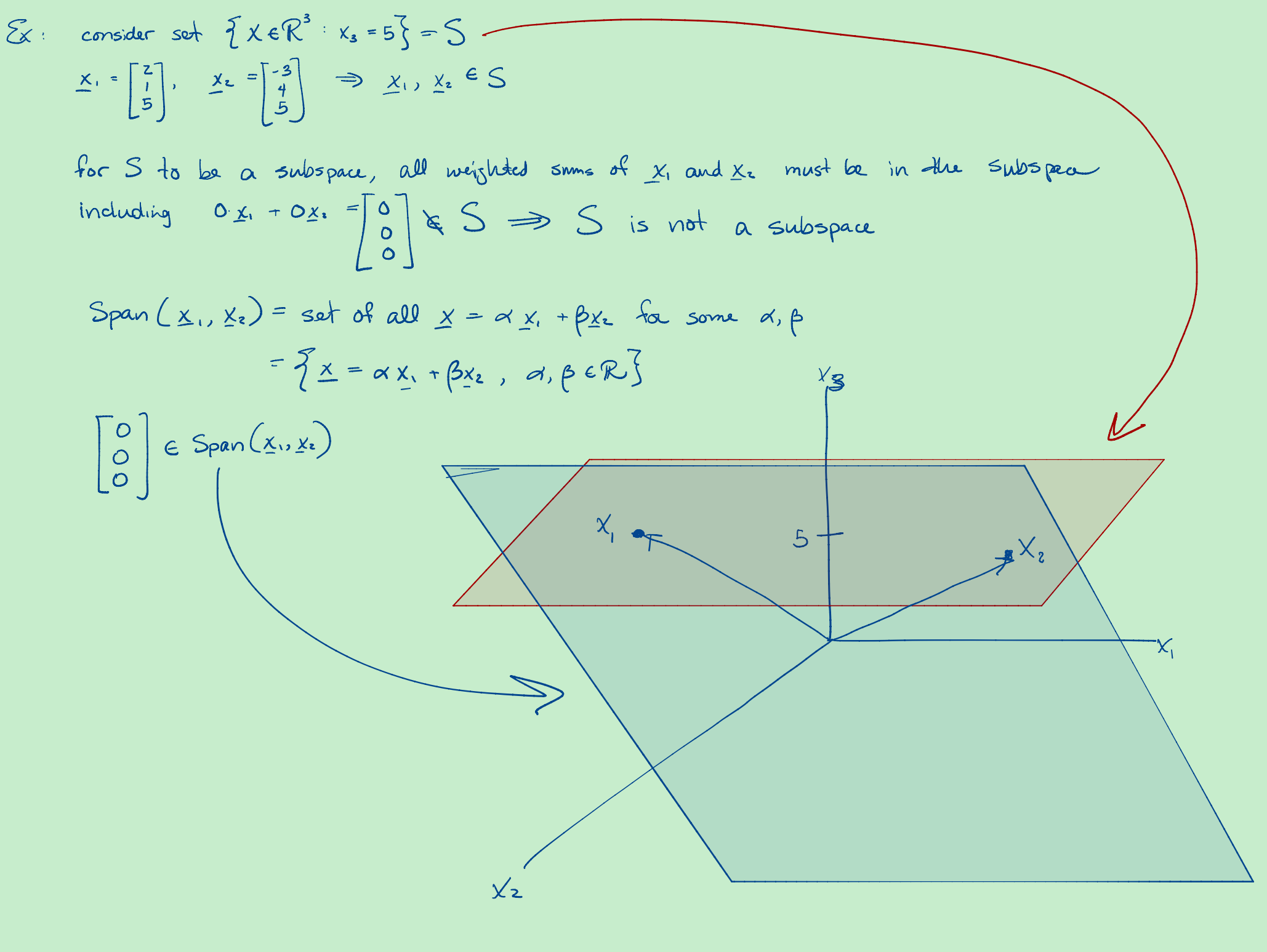

注意:最后一行。







