Lecture 4 Least squares and Optimization
Lecture 4 Least squares and Optimization
1. 最小二乘估计

最小二乘估计(上节课没讲的):
如果列向量都是线性无关的找到最小化残差和的$w$是:
其中,$(X^TX)^{-1}X^T$又叫pseudo-inverse, 伪逆。
$P_{Xy}$投影$y$到$X$上。
2. 最小二乘法分类

二分类就是把$
3. 优化方法
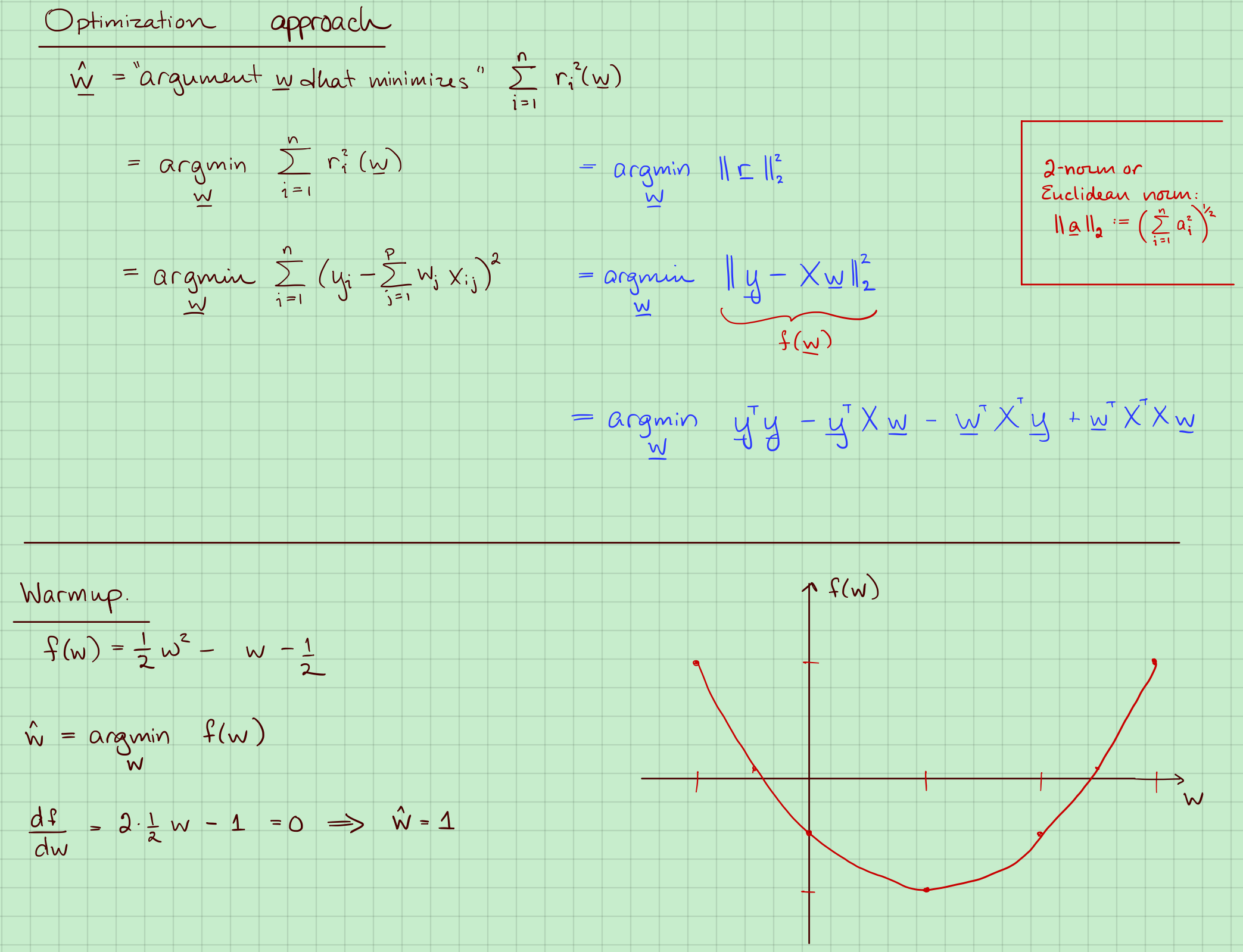
2范数或者欧几里得范数:
所以:
$y^TXw和w^TX^Ty$都是标量,而且是一样的。
Warmup:$f(w) = \frac{1}{2}w^2-w-\frac{1}{2}$。求导求极值点。
4. 正定矩阵

我们需要$X^TX$是可逆的。
从优化的角度来看这个问题。$X^TX$是正定的
正定矩阵定义:
1. 详解正定矩阵的作用和凸优化
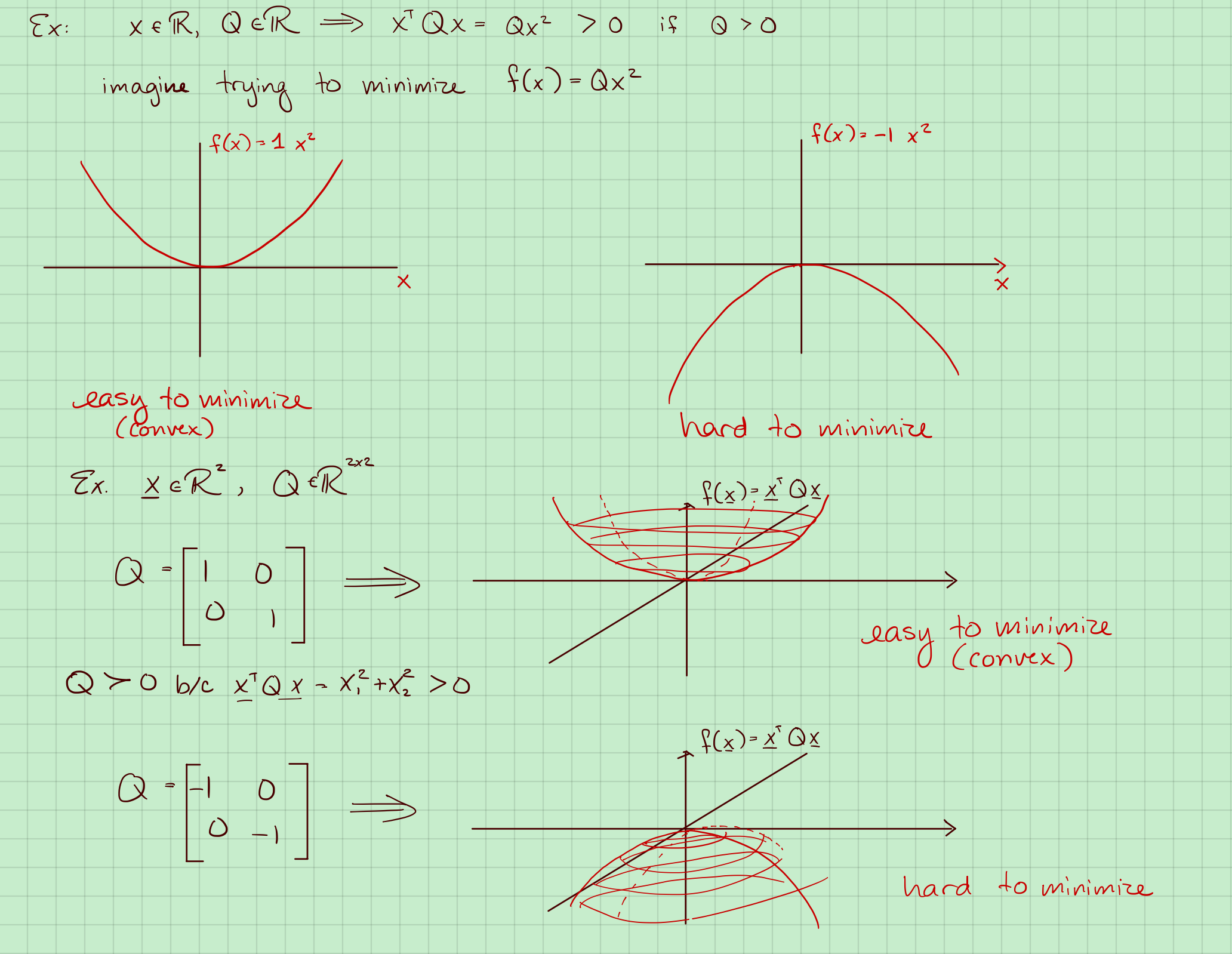
2. 正定矩阵的性质

性质3:
对于任意矩阵$A$,那么$A^TA \ge 0 $和$AA^T \ge 0 $
5. 最优化最小二乘法

假设$X^TX > 0$,那么:$f(w)=y^Ty-2w^TX^Ty+w^TX^TXw$是凸的。
计算其导数,让其等于0来求最小值。
例如$f(w) = c^Tw=c_1w_1+c_2w_2+ \cdots+c_pw_p$
其梯度为:
例如$f(w) =w^Tw=\lVert w\rVert^2_{2}=w^2_1 + w^2_2 + \cdots+ w^2_p$
总结,
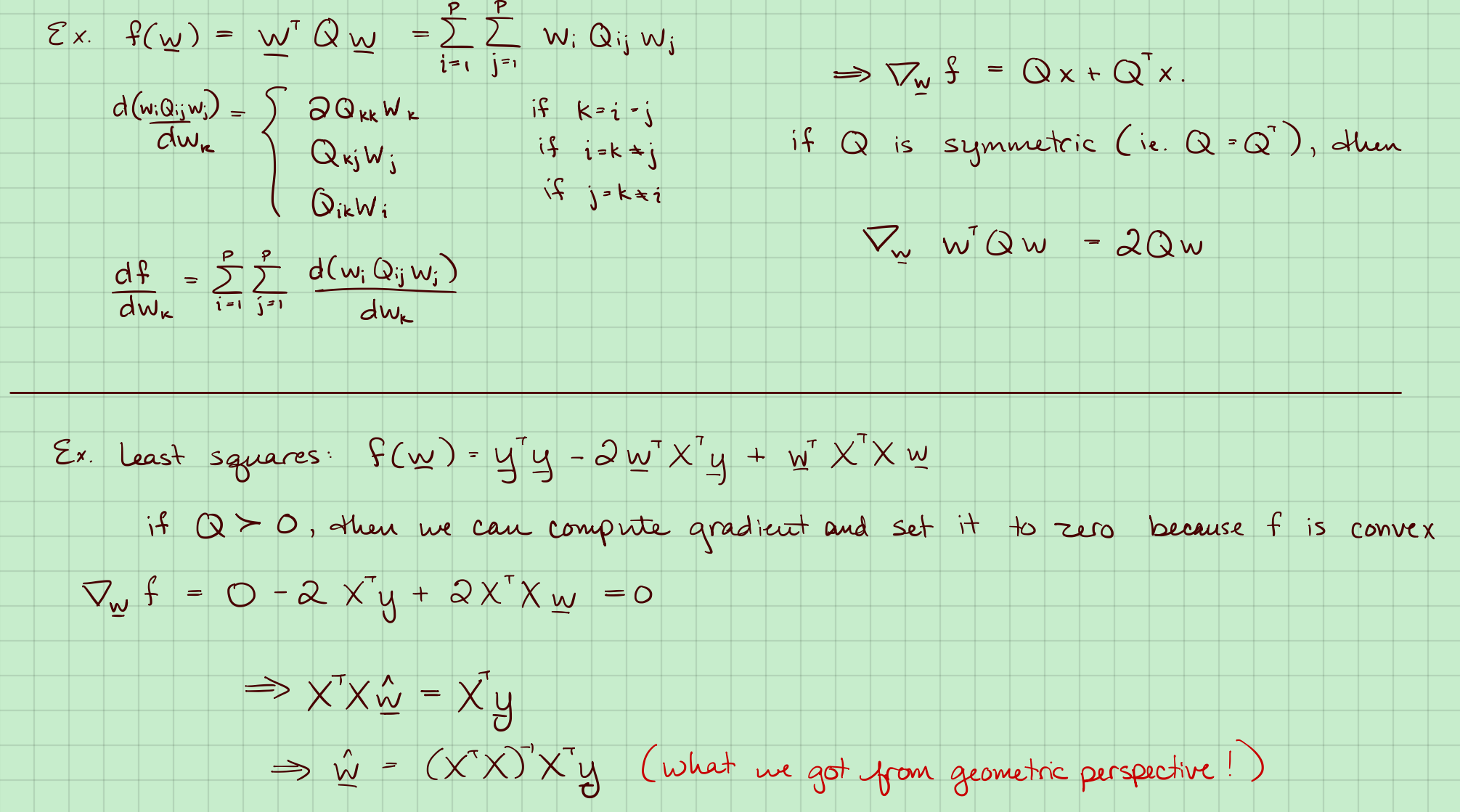
例子:
那么对$w$的梯度有下面四种情况:
这需要把$\boldsymbol{w}^TQ\boldsymbol{w}$展开来理解,下面用一个具体的例子,其中:
其部分展开得:
上式,
- 第一种情况,可以结合式7中第二个式子理解,$\boldsymbol{w}_k都是变量$。
- 第二种情况,可以结合式7中第一个式子理解,$\boldsymbol{w}_k$是变量,$\boldsymbol{w}_j$是常量。
- 第三种种情况,可以结合式7中第一个式子理解,$\boldsymbol{w}_k$是变量,$\boldsymbol{w}_i$是常量。
- 不含变量$\boldsymbol{w}_k$都是常量。
所以:
回想下简单的公式:
那么:
如果$Q$是对称矩阵($Q=Q^T$):
而$f(w)=y^Ty-2w^TX^Ty+w^TX^TXw$,其梯度为:
令其为0,同样可得:
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 aigonna!
评论






