Lecture 3 Least squares and geometry
Lecture 3 Least squares and geometry
1.最小二乘法
目标:从一些特征向量$x$学到预测标签$y$。建立一个线性模型,
需要找到$w$来使得$\hat y_i = y_i \quad for i = 1, 2, \cdots, n$
1.最小二乘法怎么来的?
因为残差residual error为:
找到最小化残差和的$w$。(式2中第一个式子,第二个式欧式距离)
提到$l_p$Norm,对于向量$r$,对其每一个元素的$p$次幂求和再开$p$次方:
2.为什么用最小二乘法?
- 正负残差同样处理
- 数学上便利
- 好的几何表示
- 放大了大误差影响
- 和高斯模型噪声一致

1.1 张成空间 Span

1.2 最小二乘的几何意义
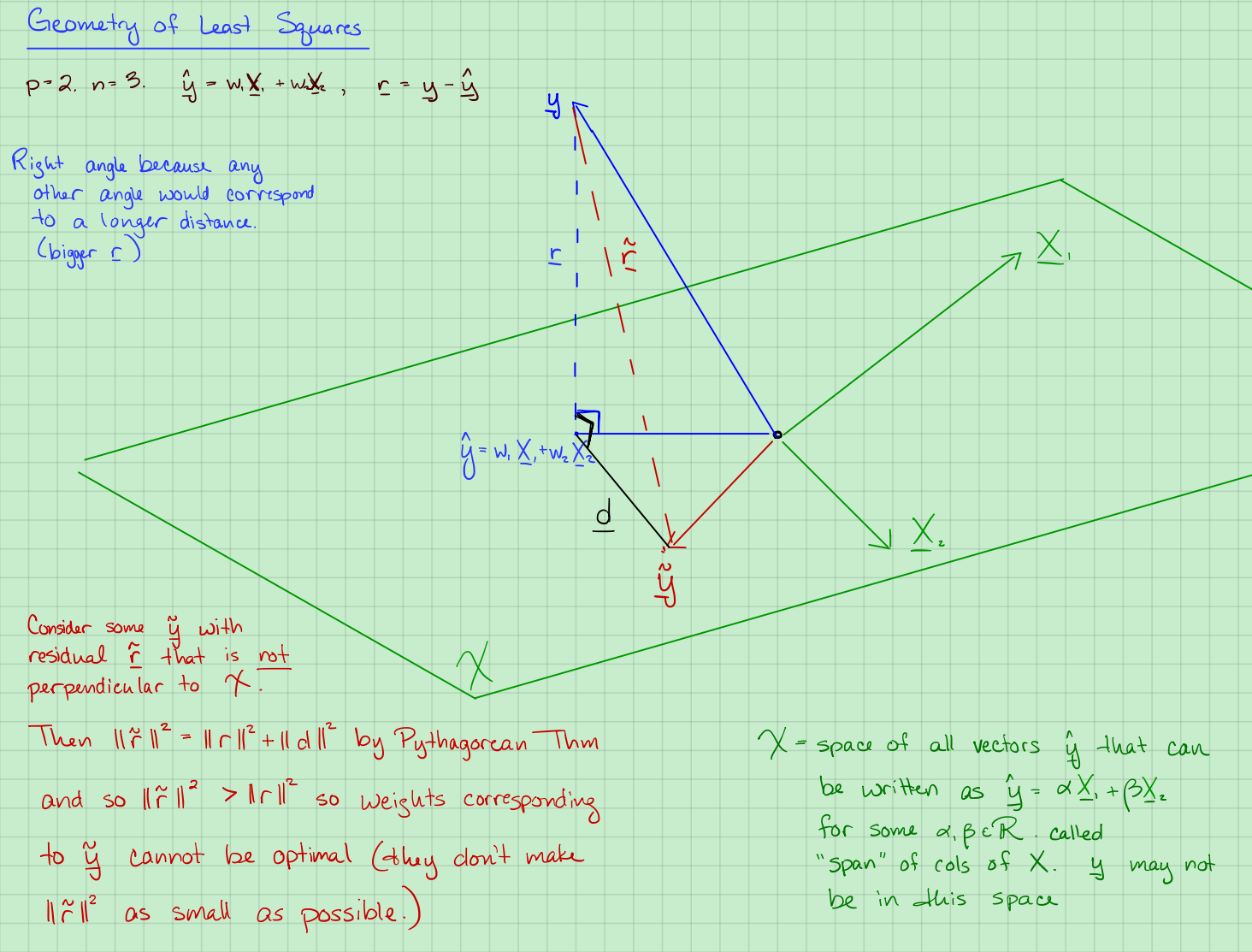
最小二乘的几何意义:
$n=3, p = 2$即3个样本,2个特征,那么:
图中的蓝色$\underline y$就是真实值,考虑对$X$的列向量的张成空间,一些$\tilde{ \underline y}$不是$\hat {\underline y}$(残差不是垂线或向量不正交)。而且有:
那么$\lVert \tilde{ r} \rVert^2>\lVert r \rVert^2$,即这不是最优的一组$w_1, w_2$。
1.3 最小化残差向量

由上面的几何证明可以知道残差向量是要与$X$的列向量张成空间垂直才最小化。那么有:
接下来我们想想是不是存在$\hat {\underline w}$使得线性方程组$X^Ty=X^TX\hat {\underline w}$成立?它是不是唯一?
1.4 线性方程组

线性方程组是否有解?
有唯一解,无穷解,无解?
1.5 线性无关

线性无关的定义:
若向量 是线性无关的,那么 当且仅当对于所有的 , 时成立。

线性相关
这里讲了一个非常重要的概念,矩阵的秩rank。
矩阵的秩:线性无关列向量的数目=线性无关行向量的数目
如果$X^T = [x_1, x_2, \cdots, x_n] \in \mathbb{R}^{p \times n}$,那么$rank(X) \leq min(p, n)$。如果$rank(X) = min(p, n)$,那么矩阵满秩full rank。
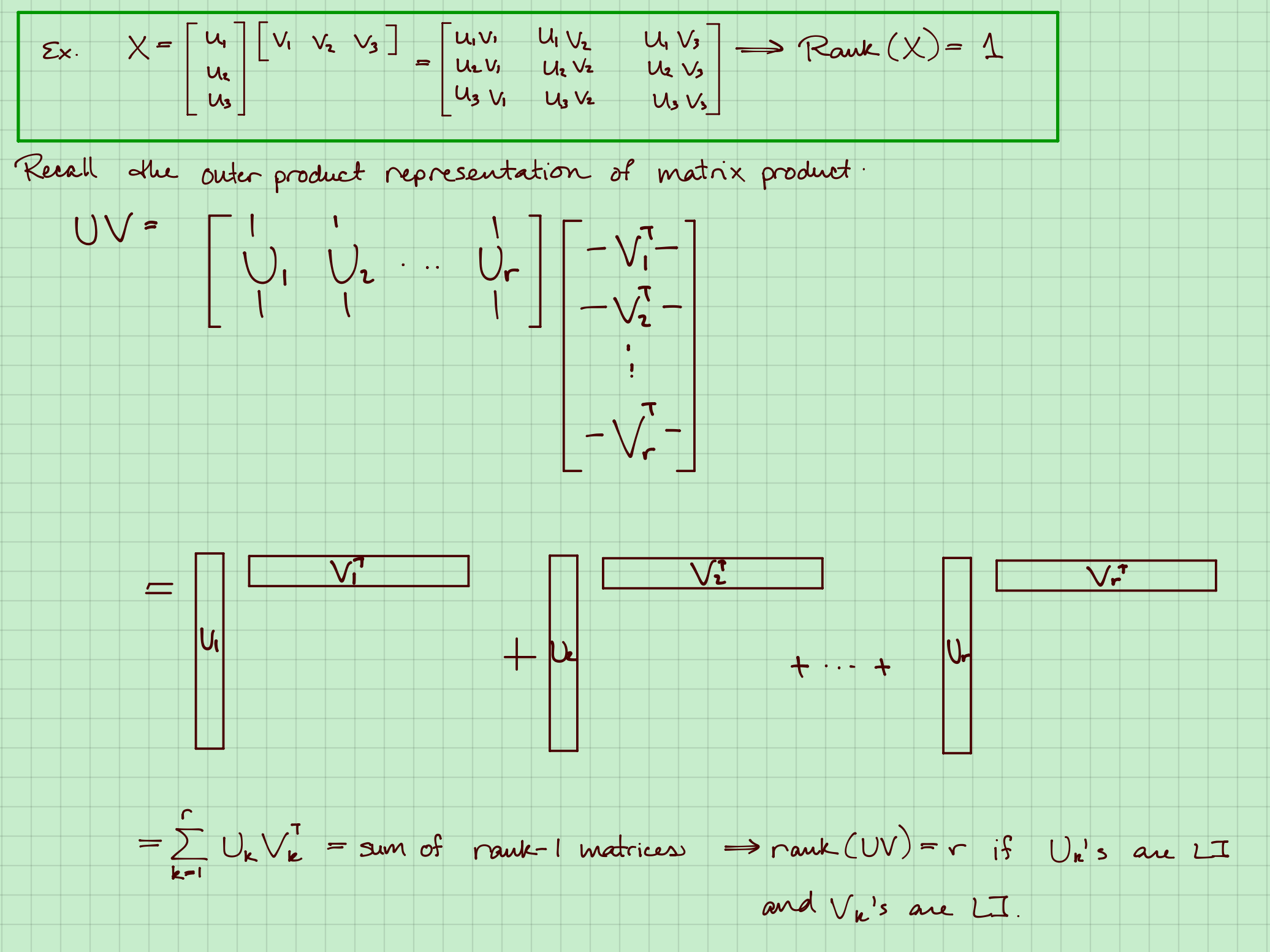
1.6 矩阵的逆(只有方阵有逆)

不是所有矩阵都有逆矩阵。只有矩阵是满秩矩阵,那么它才可能有逆矩阵。
若$X \in \mathbb{R}^{n \times p}$,假设$n \geq p , rank(X)=p$($X$有$p$个线性无关的列或者说特征), 就有$rank(X^TX)=p \Rightarrow X^T X$ 有逆矩阵。
理由:
- 因为$rank(X^TX)\leq min(p, p)=p$,那么$X^TX$有$p$个线性无关的列或者说行,所以矩阵有逆。
- $rank(X^TX)\leq min(p, p)=p$, $X^TX$是满秩矩阵,就有逆矩阵
1.7 最小二乘线性方程组是否有解?

$X^{T}(y-X \hat {\underline w})=0
\Rightarrow X^Ty=X^TX\hat {\underline w}$中,由于$n \geq p$,那么$rank(X^TX)\leq min(p, p)=p$是满秩的,$X^TX$存在逆。
可以推出:







