Lecture 2 Vectors and Matrices in Machine learning
Lecture 2 机器学习中的向量和矩阵
1. 线性模型

我们可以理解$X_i \in \mathbb{R}^p$为$p$个一系列的数值特征,一般写作一个列向量。
从训练数据,对于新的新样本$X_0$学习如何预测标签(或者目标值)$\hat{y}$。
例如线性模型,
using training data to find $W$, such that} $\hat{y_i}\approx y_i, \ for \ i=1, \ldots, n $ . want $L(\hat{y_i}, y_i) $smallest
权重向量weights vector:
特征向量feature vector:
我们的模型就可以写作内积的形式。
例子1 线性模型

竖轴是第二个特征维度,横轴是第一个特征维度。蓝色直线代表所有在
的点。
我们也可以看作: 。我们不防把第一个元素看作1,那么就有:
也可以像前面一样写成内积形式。
接下来就是最小化损失函数。
线性模型的矩阵表示矩阵表示

例如$x{21}$表示第二个训练样本的第1个特征。$x{12}$表示第一个训练样本的第二个特征。
$X^T$变成$p$行$n$ 列。
式6,矩阵$X$的第$i $行row代表: 第$i$训练样本的$p$个特征。
矩阵$X$的第$j $列col代表:所有 $n$个训练样本的第$j$个特征。
这就是不同角度看待$X$矩阵。
计算$Xw$意味着:作$X$每一行和$w$作内积然后把结果用向量$\hat y$保存下来。
教授Rebecca Willett非常详细讲了矩阵行列之间的变化关系。体会矩阵shape的变化,这对代码中间的debug非常有用.
例子 2:深刻理解Xw

上面其实是从2个角度来看矩阵乘法:行向量和列向量。
行向量角度是我们线代教材常说的,列向量有时候会让计算非常简单。(MIT线代课程,Gilbert Strang讲的非常详细。)
列向量角度:$Xw$表示$X$的列的权重之和。
例子3:复杂结构的线性模型

This doesn’t look like a straight line,but linear models can still help!
cubic polynomial:三次多项式。
范德蒙矩阵:
2. 矩阵与矩阵相乘
1. 例子:推荐系统


推荐系统
电影名 观众名 数字是评分
把矩阵$X$写作矩阵$U*V$,其中$X \in n\times p , U \in n\times r,V \in r\times p $。
矩阵$U$是对于$r$个示例电影的顾客$r$不同评分向量;$v$是每个实际顾客对$r$示例电影的相似度。
If $X= UV$,那么
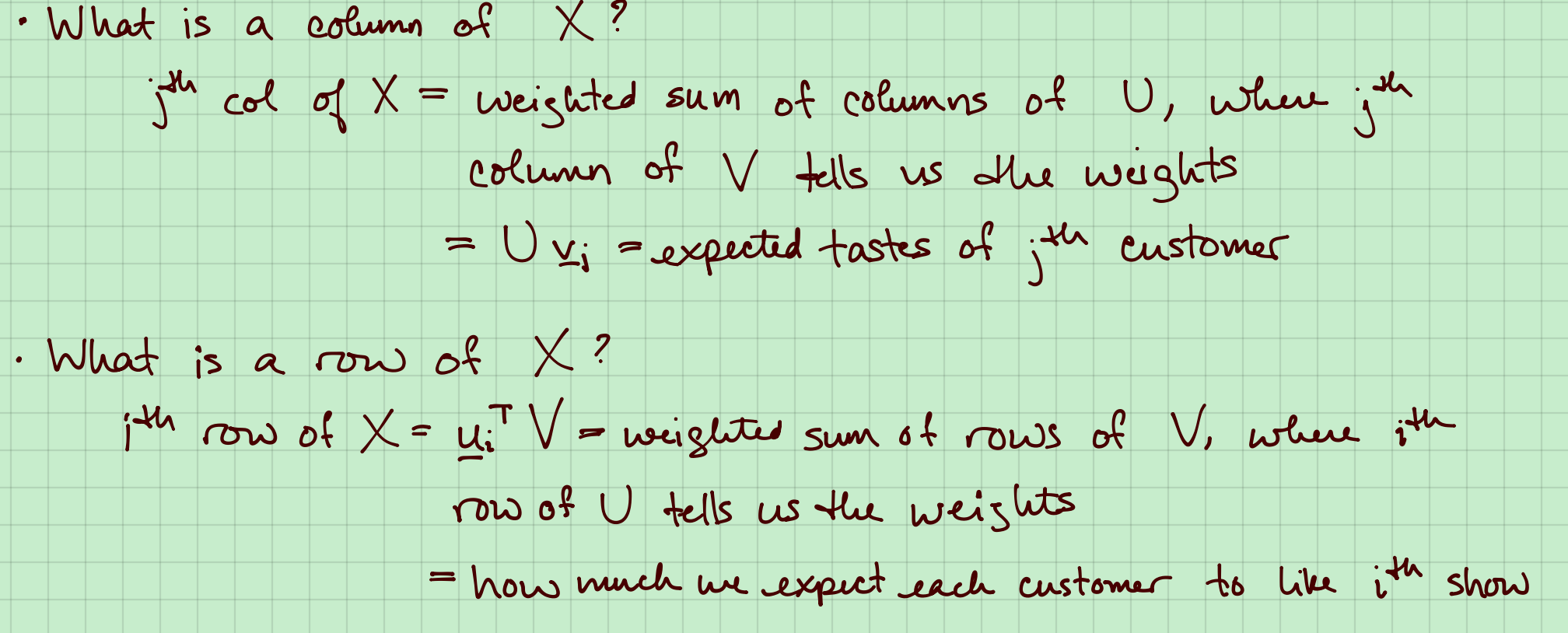
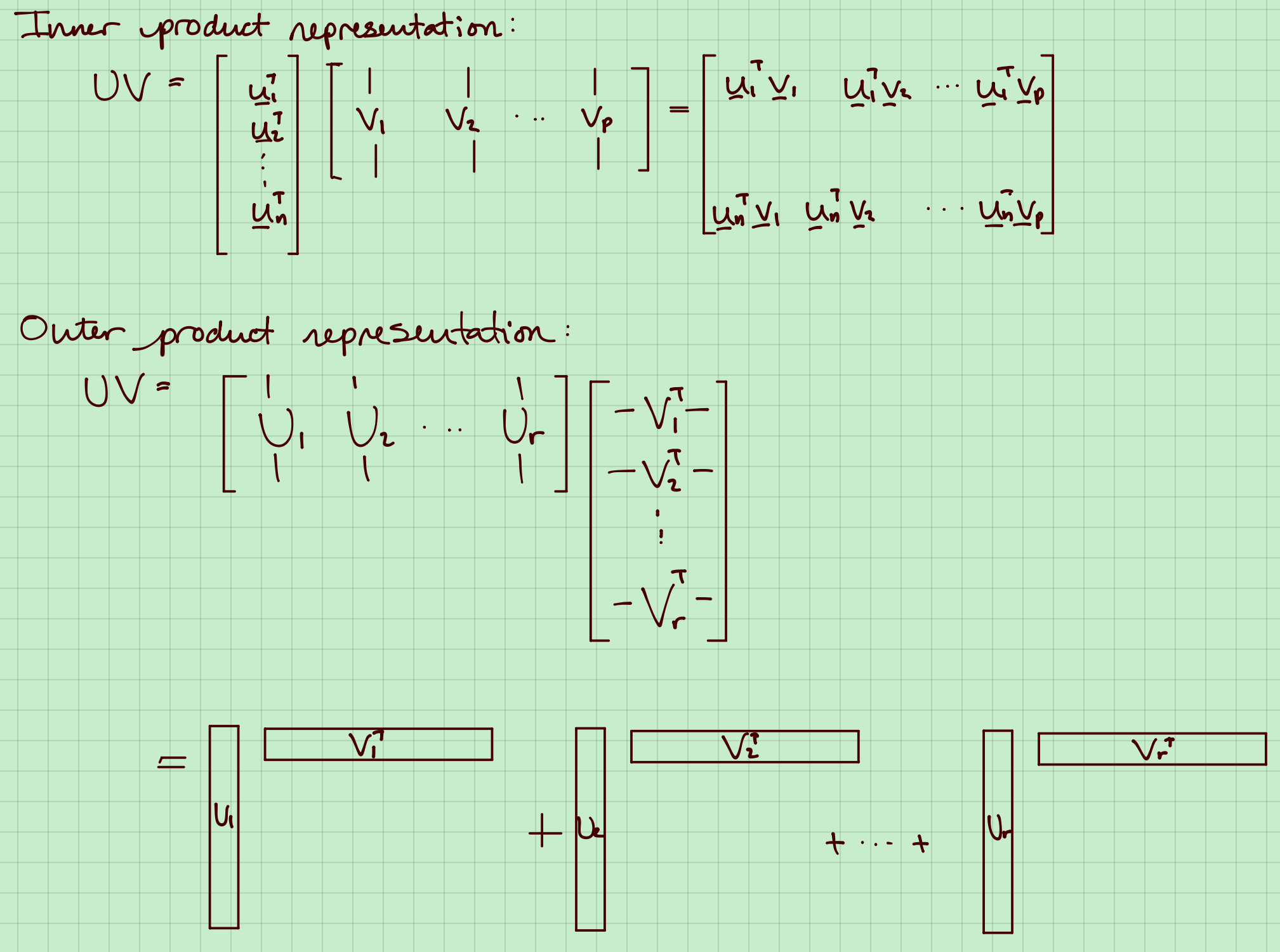
2. 内积和外积表示
3.怎么找到最小的r








