1. 二叉树

1.术语

根节点：非空树中无前驱节点的节点
节点的度：节点拥有的子树数
树的度：树内各节点的度的最大值
节点的子树的根称为该节点的孩子，该节点称为孩子的双亲；
节点的祖先：从该节点到根所经分支上的所有节点
节点的子孙：以某一节点为根的子树中的任一节点。
树的深度：树中节点的最大高度

2.二叉树应用

数据压缩
二叉树求解表达式的值

3. 二叉树的定义

二叉树是n(n≥0)个节点的有限集，它或者是空集(n=0)，或者由一个根节点及两颗互不相交的分别称作这个跟的左子树和右子树的二叉树组成。

特点：

每个节点最多有俩孩子(二叉树中不存在度大于2的节点)
子树有左右之分，其次序不能颠倒
二叉树可以是空集合，根可以有空的左子树或空的右子树

注： 二叉树不是树的特殊情况，它们是两个概念。

二叉树要区分左子树和右子树。树的话只有一个孩子时无须区分左右。

4.二叉树的性质和存储结构

性质1：在二叉树的第i层上最多有$2^{i-1}$个节点($ i \ge 1$)。第i层上至少有1个节点

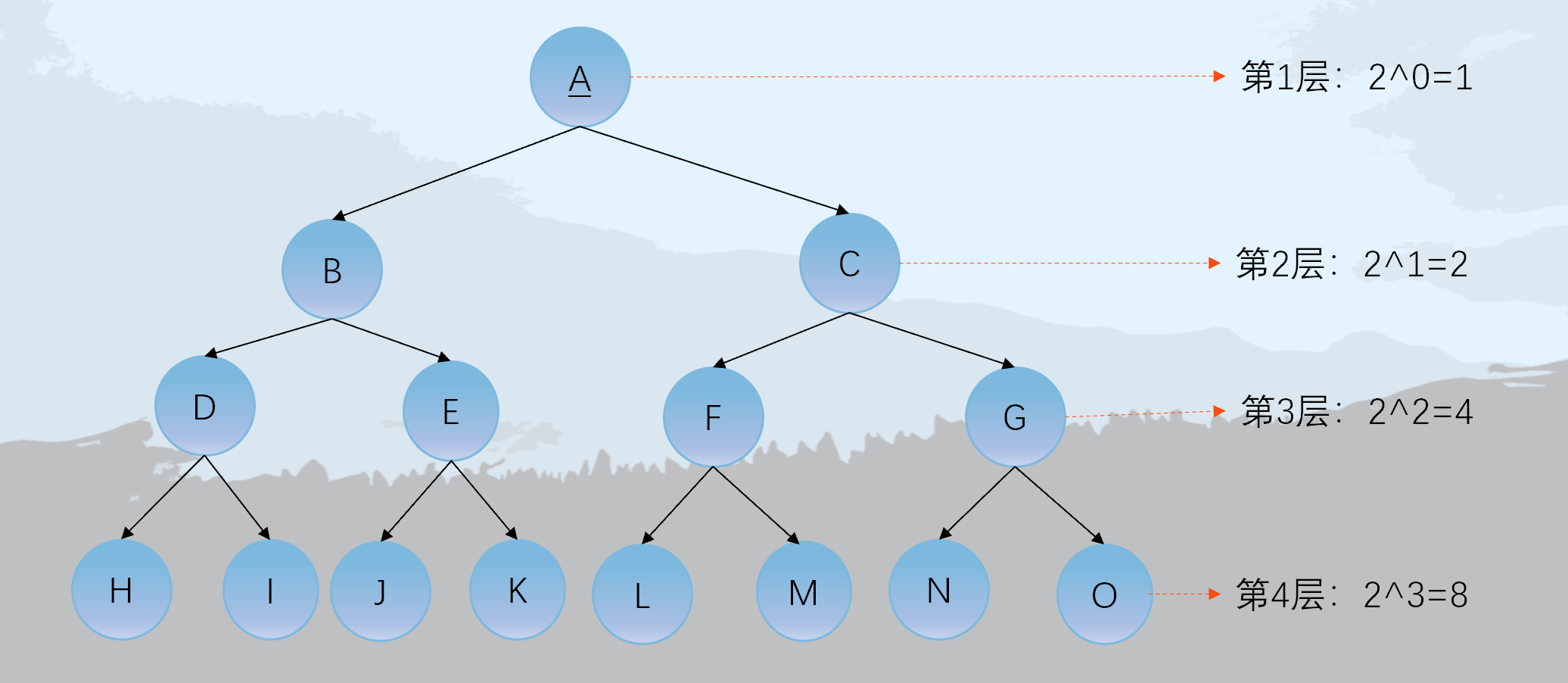
性质2：深度为k的二叉树至多有$2^k - 1= \sum_{i=1}^k 2^{i-1}$个节点, 至少要有k个节点.

性质3：对于任何一棵二叉树T，如果其叶子树为$n_0$, 度为2的节点数为$n_2$,则$ n_0 = n_2 + 1 $

证明：

总边数设为E，那么$E = n-1 \ 其中n 为节点总数$, 从下往上看

那么，$E = n_1 + 2n_2$ 度为1的有两条边，度为2的有两条边。从上往下看

那么，$n = n_1 + 2n_2 +1 = n_1 + n_2 + n_0$

5. 完全二叉树

满二叉树：一棵深度为k且有$2^k - 1$个节点的二叉树是满二叉树。跟上图一样，就是每个节点都有2个分支，度都为2.
- 特点：1.每一层上的节点数都是最大节点数(即每层都是满的)；2. 叶子节点全部都在最底层
- 编号规则：从根节点开始，从上而下，自左向右。
- 满二叉树在同样深度的二叉树中节点个数最多
- 满二叉树在同样深度的二叉树中叶子节点个数最多
完全二叉树：深度为k的具有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号为1~n的节点一一对应时，称为完全二叉树。

下图是完全二叉树。

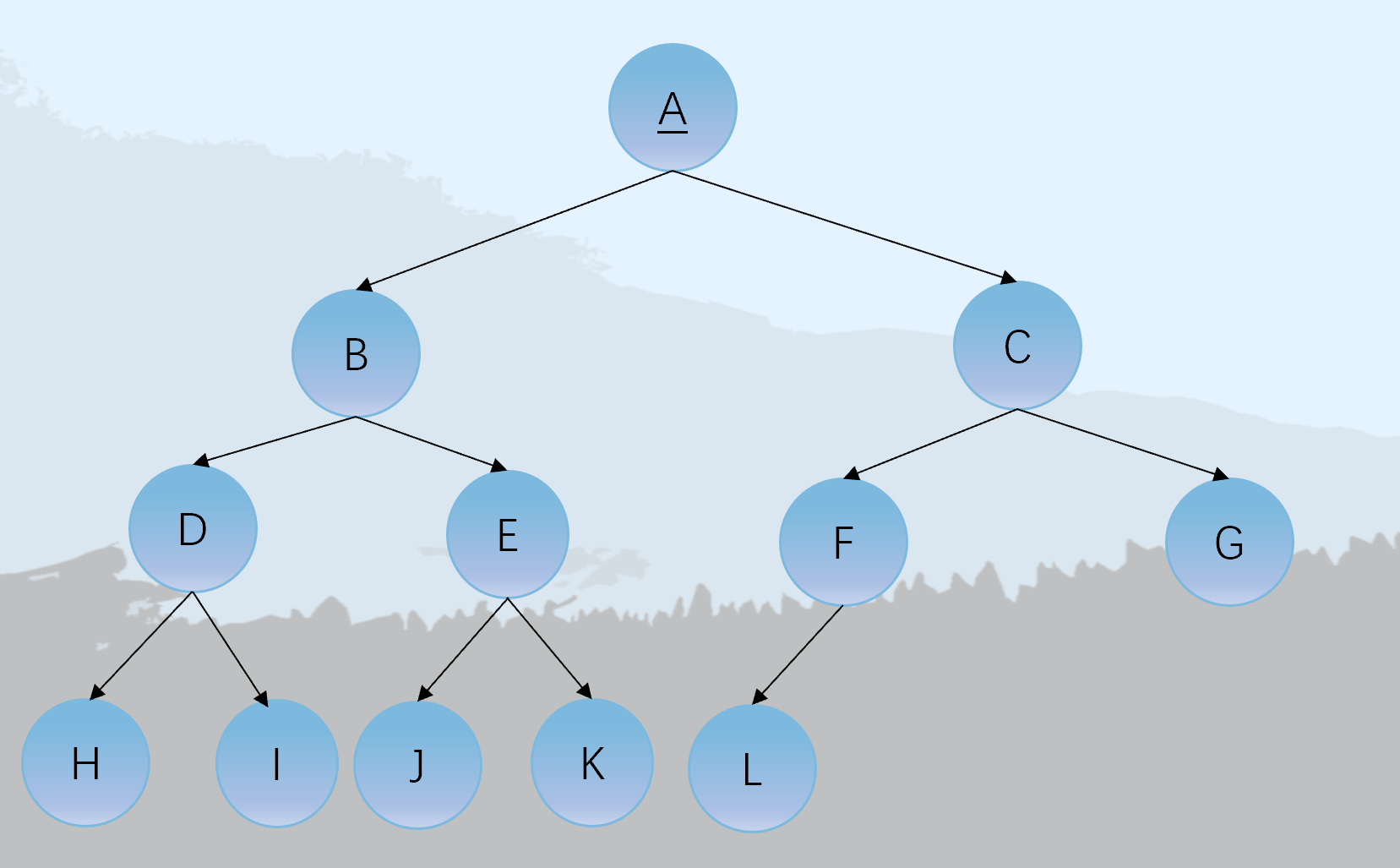
注：在满二叉树中，从最后一个节点开始，连续去掉任意个节点，就构成了一个完全二叉树

特点：

叶子只能分布在层次最大的两层上
对任一节点，如果其右子树最大层次为i，则其左子树的最大层次必为$i或i+1$

则其左子树的最大层次必为$i或i+1$

完全二叉树性质：

性质：

具有n个节点的我完全二叉树的深度为 $ \text{floor }(\text{log}_2n)+ 1 $.得到深度与节点数的关系
如果对一棵有n个节点的完全二叉树(深度为$ \text{floor }(\text{log}_2n)+ 1 $)的节点按层序编号，从第一层到第$ \text{floor }（ \text{log}_2n）+ 1 $层，每层从左到右，则对任一节点$1 \le i \le n$有：(父节点和孩子节点编号关系)
- 如果$i=1$,则节点$i$是二叉树的根，无父节点，如下图节点1；如果$i \gt 1$,则其父节点是节点 $ \text{floor }(i/2) $，如节点2或3
- 如果$2i \gt n$,则节点$i$为叶子节点，无左孩子；否则其左孩子是节点$2i$
- 如果$2i+1 \gt n$，则节点$i$无右孩子；否则其右孩子节点是$2i+1$

6. 二叉树的存储结构

二叉树的顺序存储：

实现：按满二叉树的节点层次编号，依次存放二叉树中的数据元素。

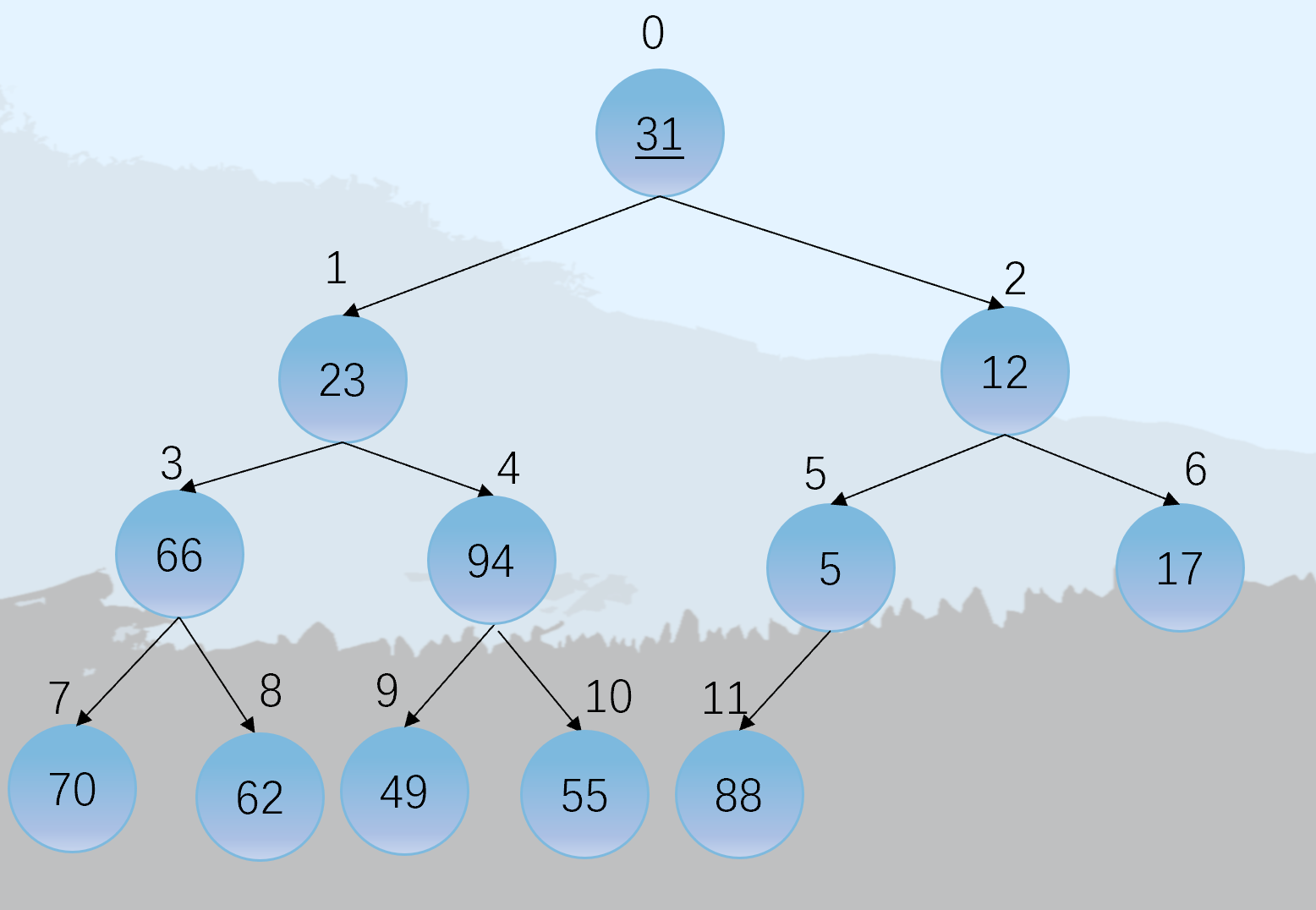
其编号和存储元素为：

0	1	2	3	4	5	6	7	8	9	10	11
31	23	12	66	94	5	17	70	62	49	55	88

但如果不是完全二叉树呢?如下图，依旧按满二叉树编号，没有的存储元素为空。

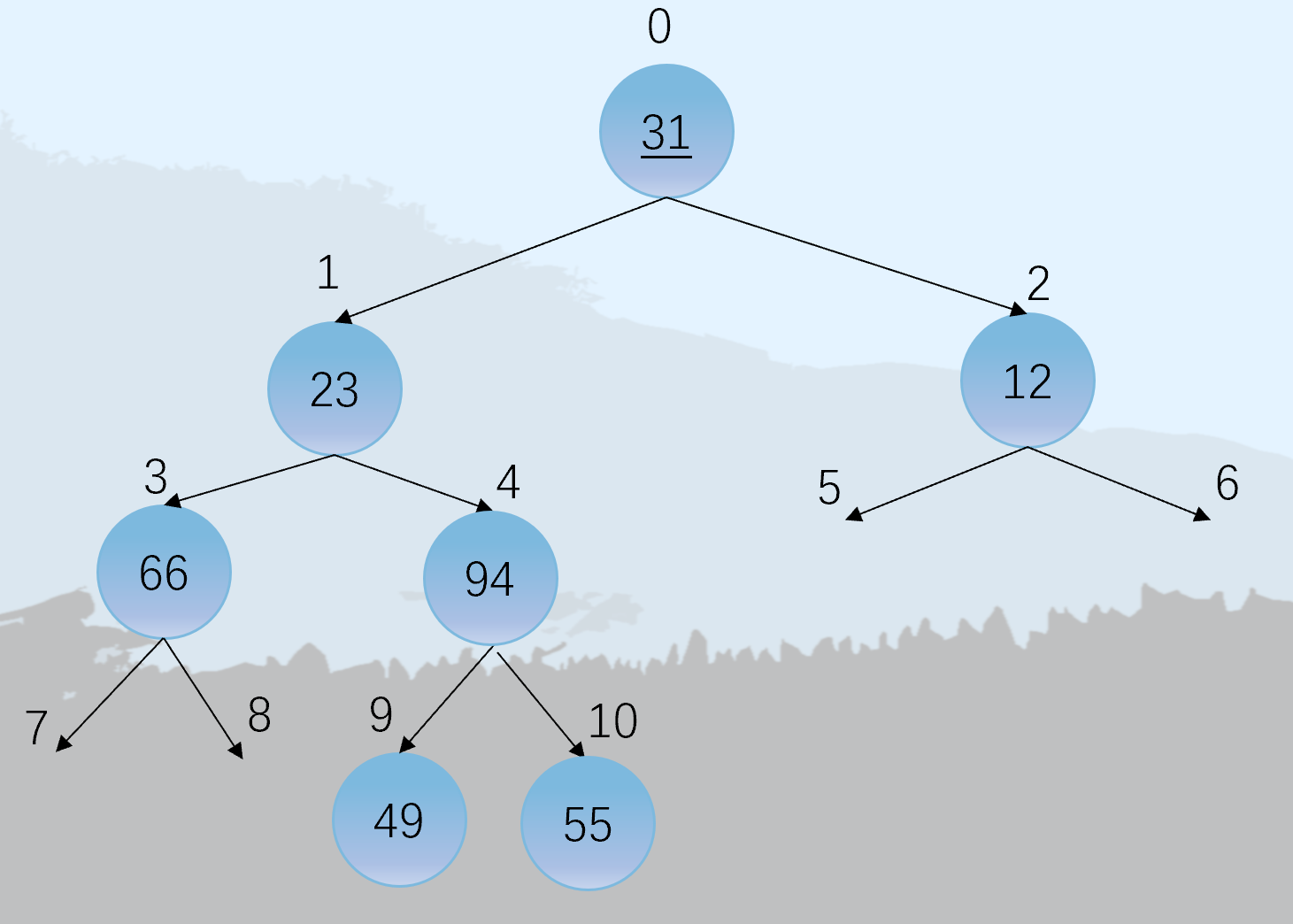
其编号和存储元素为,

0	1	2	3	4	5	6	7	8	9	10
31	23	12	66	94					49	55

顺序存储的缺点：

元素大小固定
出现空节点时，相应位置浪费存储空间。最坏情况：深度为k的且只有k个节点的单支树需要长度为$2^k - 1 $的一维数组。(右单支树)

特点：节点间关系蕴含在其存储位置中，浪费空间，适于满二叉树和完全二叉树。

二叉树的链式存储结构

注:在n个节点的二叉链表中，有n+1个空指针域

因为n个节点，那么有2n个链域。(这是从根往叶子节点看)。反过来看，每个节点必有一个指针，除了根节点。那么空指针域有$2n-(n-1)=n+1$

2. 二叉树的遍历

遍历的定义：顺着某一条搜索路径访问二叉树中的节点，使得每个节点均被访问异常，而且仅被访问一次.

遍历的目的：得到树中所有节点的一个线性排列

遍历的用途：它是树的结构插入、删除、修改、查找的基础

共有6种遍历方式：D：根节点 L:左节点 R：右节点

DLR、LDR、LRD、DRL、RDL、RLD

前序遍历：DLR

中序遍历：LDR

后序遍历： LRD

递归进行遍历。

前序遍历：若二叉树为空，则空操作；否则：

访问根节点
前序遍历左子树
前序遍历右子树

下图二叉树的3中遍历顺序：

前序遍历： ABELDHMIJ（根左右）

中序遍历： ELBAMHIDJ (左根右)

后序遍历： LEBMIHJDA (左右根)

再练习下图二叉树3种顺序遍历：

二叉树表示算术表达式：

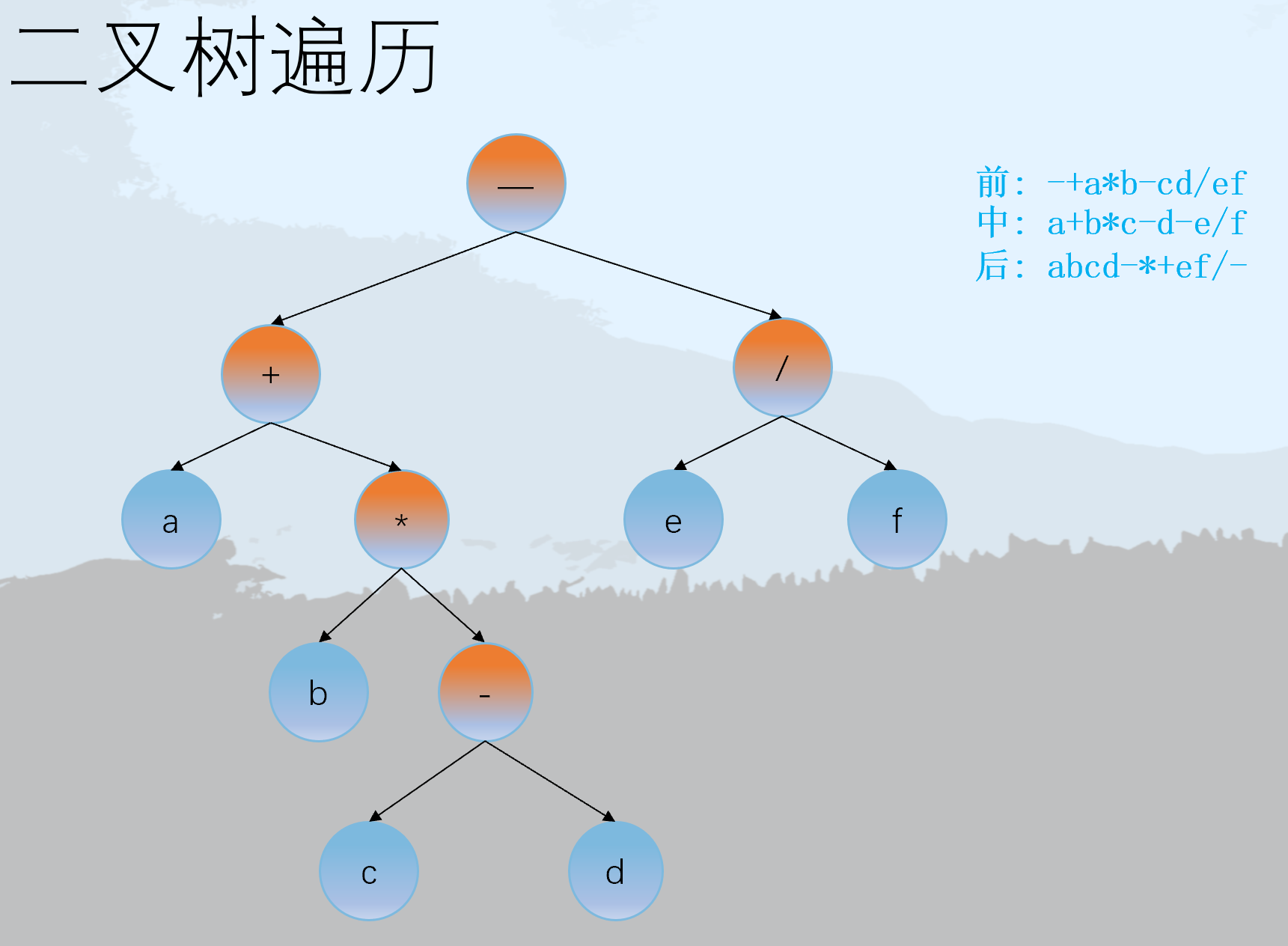
前序遍历中运算符在前面，称作前缀表示

中序遍历中运算符在中间，称作中缀表示

后序遍历中运算符在后面，称作后缀表示

前序和中序确定二叉树

如果要根据前序和中序遍历结果求二叉树，关键点是：前序确定根，中序确定左右子树。

例如：已知

先序： A B C D E F G H I J
中序： C D B F E A I H G J

由先序确定A是整个的根，根据中序： CDBFE是左子树部分， IHGJ是右子树。

在CDBFE中，先序先遍历B，那么B是这部分的根；再看中序 CD是左， FE是右；再对CD而言，先序遍历是CD，中序是CD，(根左右，左根右)那么只能是C为B的左子树，D为C的右子树。

在IHGJ中，先序先遍历G，那么G是这部分的根；再看中序， IH是左， J是右。结果如下：

中序和后序确定二叉树

中序： BDCEAFHG

后序： DECBHGFA

根据后序最后是根来确定根，根据中序确定左右。

1. 中心遍历非递归算法

二叉树中序遍历的非递归算法的关键：在中序遍历过某个节点的整个左子树后，如何找到该节点的根以及右子树

基本思想:(遇到根时先不访问，先入栈；先访问左子树，等访问完；再访问根，就把根节点出栈；最后访问右子树。）

建立一个栈
根节点进栈，遍历左子树
根节点出现，输出根节点，遍历右子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        st, ans = [], []  # 节点暂时存储的栈，结果
        cur = root  # 当前指针
        while st or cur:  # 当栈或当前节点不为空
            if cur:  # 如果当前节点不为空
                st.append(cur)  # 栈压入当前节点
                cur = cur.left  # 当前指针指向左子树
            else:  # 栈不空
                cur = st.pop()  # 当前指针指向栈顶
                ans.append(cur.val)  # 栈顶值加入ans
                cur = cur.right  # 当前指针指向右子树
        return ans

2. 二叉树的层次遍历

设计思路：使用一个队列

将根节点入队
队不空时循环；从队列中出列一个节点*p，访问它；
1. 若它有左孩子节点，将左孩子节点入队
2. 若它有右孩子节点，将右孩子节点入队

稀碎的理解：

先入队根节点，再出队；
如果有左右孩子，将左右孩子都入队；
左孩子出队，如果左孩子还有左右孩子，继续将左右孩子入队；
右孩子也一样
直到队列为空

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        ans = []
        que = [root] # 根节点入队
        while que: # 队列不空
            tmp = []
            for i in range(len(que)):
                cur = que.pop(0) #指向队列第一个元素
                tmp.append(cur.val) #将当前值加入ans
                #开始访问其左右子树
                if cur.left:
                    que.append(cur.left)
                if cur.right:
                    que.append(cur.right)
                
            ans.append(tmp)
        return ans

3. 二叉树遍历算法的应用

1. 二叉树的建立

如先序遍历得到字符如ABC##DE#G##F###；

先判断输入字符是不是#,如果是，将当前指针置为空
不是#时，先生成根节点
再依次生成左右子树

题目：1008. 前序遍历构造二叉搜索树

稀碎的想法：

如果前序列表为空，直接返回None
先将树添加前序的第一个元素，并将root指向Tree，这样就形成了root为整个树的根节点
遍历前序列表中剩余元素，如果小于root值就是左子树，大于就是右子树
但上面左右子树是一个大的左子树，右子树也是，将其分别看作一个小的子树，再遍历就好了

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def bstFromPreorder(self, preorder: List[int]) -> TreeNode:
        if not preorder:
            return None
        # 当前指针置为树节点的根节点，前序遍历第一个元素为整棵树的根
        root = TreeNode(preorder[0])
        left, right = [], [] #两个列表分别放左右子树
        for x in preorder[1:]: #遍历前序列表1:n
            if x < root.val: #如果元素小于根节点，左子树
                left.append(x) #左子树元素加入左子树列表
            else: 
                right.append(x)
        root.left = self.bstFromPreorder(left) #递归遍历左子树
        root.right = self.bstFromPreorder(right) 
        return root

2. 复制二叉树

基本思路：

如果是空树，返回None
不是；申请新节点空间，再复制根节点
- 递归复制左子树
- 递归复制右子树

#include<cstdio>
#include<iostream>

struct treenode//结点的定义
{
    int data;
    treenode* left;
    treenode* right;
};

typedef treenode* Tree;

Tree CopyNode(Tree t)//复制结点t
{
    Tree newT = (Tree)malloc(sizeof(treenode));
    newT->data = t->data;
    newT->left = t->left;
    newT->right = t->right;
    return newT;
}

Tree CopyTree(Tree t)
{
    if(!t)
        return NULL;//树为空，直接返回NULL

    Tree newLeft = NULL,newRight = NULL,newTree = NULL;
    if(t->left)//左子树不为空则复制左子树
        newLeft = CopyTree(t->left);
    else
        newLeft = NULL;
    if(t->right)//右子树不为空则复制右子树
        newRight = CopyTree(t->right);
    else
        newRight = NULL;

    Tree NewTree = CopyNode(t);//复制左右子树的根结点
    NewTree->left = newLeft;
    NewTree->right = newRight;

    return NewTree;
}

3. 二叉树的深度

思路：

如果是空树，则深度为0；
否则，递归计算左子树的深度为m，递归计算右子树的深度为n，则二叉树的深度为m与n较大者再加1，$max(m, n) + 1$

题目：剑指 Offer 55 - I. 二叉树的深度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        """
        思路：

            - 如果是空树，则深度为0；
            - 否则，递归计算左子树的深度为m，递归计算右子树的深度为n，
                则二叉树的深度为m与n较大者再加1
        """    
        if not root:
            return 0
        else:
            return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        return depth(root);
        
    }
    int depth(TreeNode* root){
        if (root== nullptr){
            return 0;
        }
        int left = depth(root->left);
        int right = depth(root->right);
        return max(left, right)+1;
    }
};

4. 计算二叉树节点总数

如果空树，节点为0
否则，节点个数为左子树的节点个数+右子树节点个数+1

题目：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
# *   1. 如果空树，节点为0
# *   2. 否则，节点个数为左子树的节点个数+右子树节点个数+1
class Solution:
    def countNodes(self, root: TreeNode) -> int:
        if root == None: return 0
        return self.countNodes(root.left) + self.countNodes(root.right) + 1

c++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */

class Solution {
int count = 0;

public:
    int countNodes(TreeNode* root) {
        
        if (root){
            count ++;
            countNodes(root->left);
            countNodes(root->right);           
        }
        return count;
    }
};

3. 线索二叉树

1. 为什么研究线索二叉树？

当二叉链表作为二叉树的存储结构时，可以很方便地找到某个节点的左右孩子；但是一般情况下，无法直接找到该节点在某种遍历序列中的前驱和后继节点。

Q:那么如何寻找特定遍历序列中的二叉树节点的前驱和后继？

通过遍历寻找——费时间
再增设前驱、后继指针与——增加了存储负担
利用二叉链表中的空的指针域

利用二叉链表中的空的指针域的数量:

具有n个节点的二叉链表中，一共有2n个指针域；

因为n个节点中有n-1个孩子，即2n个指针域中有n-1个用来指示节点左右孩子，其余n+1个指针域为空。

2. 线索二叉树

利用二叉链表中的空指针域：

如果某个节点的左孩子为空，则将空的左孩子指针域改为指向其前驱；
如果某个节点的右孩子为空，则将空的右孩子指针域改为指向其后驱

这种改变指向的指针称为“线索”

加上线索的二叉树称为线索二叉树（Threaded Binary Tree）。

对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。

但是我们无法区分一个节点到底是指向左右孩子还是前驱后继节点，为此引入标志位。

为了区分lchild和rchild指针到底是指向孩子的指针，还是指向前驱或者后继的指针，我们增加了两个标志与ltag和rtag。并约定：

ltag = 0 : lchild指向该节点的左孩子
ltag = 1 : lchild指向该节点的前驱
rtag = 0 : lchild指向该节点的右孩子
rtag = 1 : lchild指向该节点的后继

再增加一个头结点：

ltag=0, lchild指向根节点

rtag=1,rchild指向遍历序列中的最后一个节点

遍历序列中第一个节点的lc与后最后一个节点rc与都指向头结点。

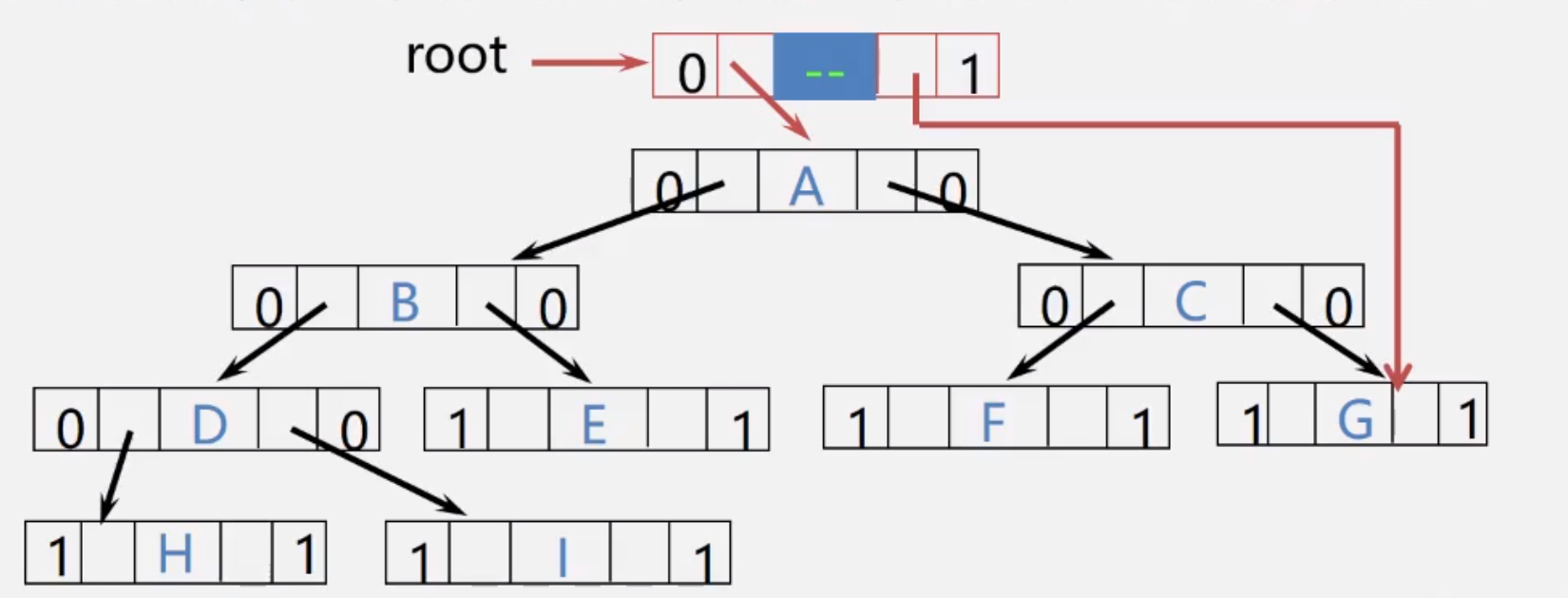
3. 线索二叉树分类

先序线索二叉树：ABCDE

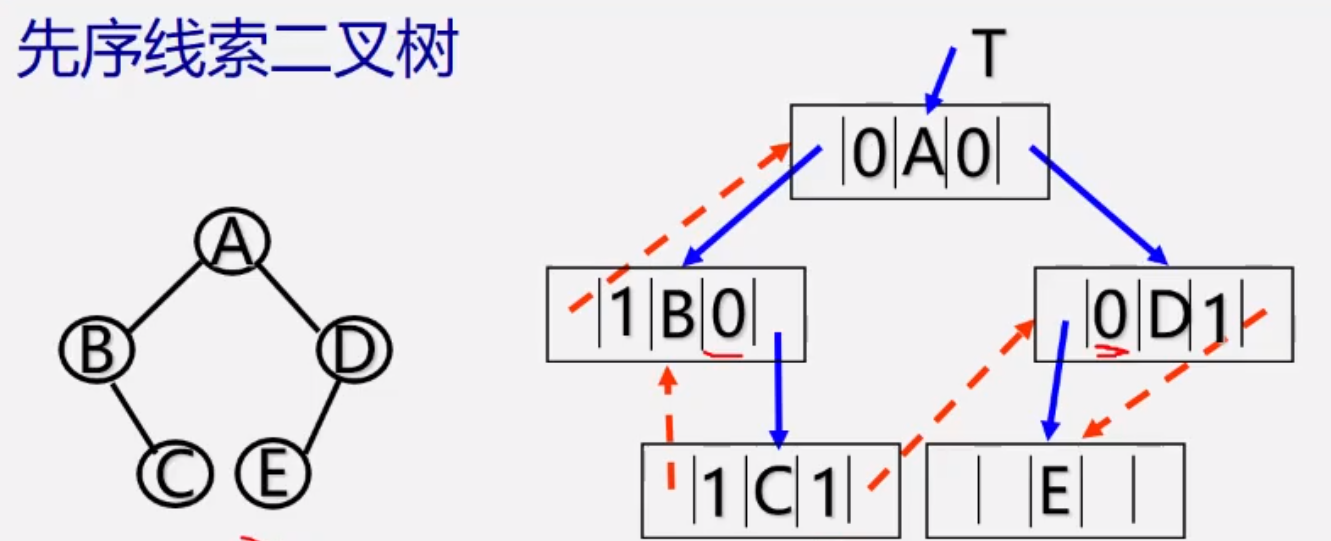
如上图中，整个线索化过程如下

A的左右孩子为BD，A的标志位都置为0，并分别指向BD
B的左孩子为空，标志位ltag=1，指向前驱A，右孩子为C，标志位rtag=0，指向C
C的左右孩子为空，标志位都置为1，并分别指向前驱B后后继D
D的孩子为E，左标志位置为0，指向E；右标志位置为1指向后继E

同样中序线索二叉树和 后续线索二叉树